Program Verification with F*
Bio
-
2007 - 2010, Tallinn University of Technology, BSc (virtualisation)
-
2011 - 2012, University of Cambridge, MPhil (computational effects)
-
2012 - 2017, University of Edinburgh, PhD (effects & dependent types)
-
2011, Tallinn University of Technology, Research Intern
(model-based testing & container datatypes) -
2014, Microsoft Research Silicon Valley, Research Intern (big data)
-
2016, Microsoft Research Redmond, Research Intern (F*)
-
2017 - 2018, Inria Paris, PostDoc (F*)
-
2018 - 2019 , University of Ljubljana, PostDoc (effects & F*)
-
2019 - . . . , University of Ljubljana, Marie Curie Fellow (effects & F*)
Plan
-
Lecture
-
Crash course in program specification and verification
-
What is F*?
-
Verification of purely functional and stateful programs in F*
-
Highlights of other F* features
-
-
Exercise class
-
Interactive live-coding and more F* examples
-
F* applied to writing verified embedded code for IoT devices
-
-
Interested in doing a dissertation in this area?
==>@Juhan & @me
Slides, code, exercises, homework, and setup instructions
https://danel.ahman.ee/teaching/taltech2020/
Do ask questions!
Specification and Verification
Program specification
- Consider a simple purely functional list reversal
let rec rev #a (l:list a) : list a = match l with | [] -> [] | hd::tl -> append (rev tl) [hd]
-
The specification of
revcould comprise a variety of properties, e.g.,rev (rev l) == llength (rev l) == length lrev lcontains the same elements asl- if
sorted (>=) lthensorted (<=) (rev l)
- Specs. are connected to programs that satisfy them using Hoare triples:
{logical precondition}program{logical postcondition}
- For example, one spec. for
rev lwould be (using an F*-like notation){requires (sorted (>=) l)} rev l {ensures (fun l' -> sorted (<=) l')}
Program specification ctd.
- Now consider a simple stateful list reversal
let rec srev #a (l:ref (list a)) : unit = match !l with | [] -> () | hd::tl -> l := tl; srev tl; l := (append !l [hd])
- The specification: previous functional properties + memory safety
- Specifications are still connected to programs using Hoare triples
- but they can now also refer to initial (
h0) and final (h1) heaps{requires (fun h0 -> sorted (>=) (sel h0 l))} srev l {ensures (fun h0 _ h1 -> sorted (<=) (sel h1 l) /\ modifies !{l} h0 h1)}
- but they can now also refer to initial (
- Memory-safety is important for composing stateful programs
{requires (fun h0 -> sorted (>=) (sel h0 l1) /\ sorted (>=) (sel h0 l2) /\ l1 =!= l2)} (srev l1) || (srev l2; srev l2) {ensures (fun h0 _ h1 -> sorted (<=) (sel h1 l1) /\ sorted (>=) (sel h1 l2))}
- Similar story also for other effects (I/O, exceptions, probability, …)
Program verification
Verifying a program is to show that it satisfies its specification, e.g.,
- Code reviews
- Testing (unit testing, randomised testing, model-based testing, …)
- Runtime verification (monitors, …)
-
Program logics (Hoare logic, separation logic, …)
{fun h0 -> sorted (>=) (sel h0 l)} srev l {fun h0 _ h1 -> sorted (<=) (sel h1 l)} {fun h1 -> sorted (<=) (sel h1 l)} srev l {fun h1 _ h2 -> sorted (>=) (sel h2 l)} --------------------------------------------------------------------------------- {fun h0 -> sorted (>=) (sel h0 l)} srev l; srev l {fun h1 _ h2 -> sorted (>=) (sel h2 l)}
-
Expressive type systems (dependent types, refinement types, …)
rev : l:list a -> (l':list a & (length l == length l'))
F* combines program logics with expressive types!
What is F*?
Program verification: Shall the twain ever meet?
| Interactive proof assistants | Semi-automated verifiers of imperative programs | |||
|---|---|---|---|---|
| Coq, | air | Dafny, | ||
| Agda, | FramaC, | |||
| Lean, | gap | Why3, | ||
| Isabelle | Liquid Haskell | |||
-
Left side: very expressive logics, interactive proving, tactics
- but mostly only purely functional programming
- but mostly only purely functional programming
-
Right side: effectful programming, SMT-based automation
- but only very weak logics
Bridging the air gap: F*
- Functional programming language with effects
- like F#, OCaml, Haskell, …
but with a much richer type systemlet incr = fun (r:ref a) -> r := !r + 1
- like F#, OCaml, Haskell, …
-
By default extracted to OCaml or F#
- (Low*) subset extracted to efficient C code (using KreMLin)
- Semi-automated verification system using SMT (Z3)
- push-button automation like in Dafny, FramaC, Why3, Liquid Haskell
- Interactive proof assistant based on dependent types
- interactive proving and tactics like in Coq, Agda, Lean, …
F* in action, at scale
-
Functional programming language with effects
- F* is programmed in F*, but not (yet) verified
-
Semi-automated verification system
- Project Everest: verify and deploy new, efficient HTTPS stack
- Verified embedded code for IoT devices (WIP with Juhan and Fabricio)
-
Proof assistant based on dependent types
How to use F*?
Using F*
-
Two kinds of F* files
-
A.fsti - interface file for module called A (can be omitted)
-
A.fst - source code file for module called A
-
- Command line: typechecking/verification
$ fstar.exe Ackermann.fst
Verified module: Ackermann (429 milliseconds)
All verification conditions discharged successfully- Command line: typechecking/verification + program extraction
$ fstar.exe Ackermann.fst --odir out-dir --codegen OCaml- Interactive: development + verification (Emacs with fstar-mode)
Verifying Purely Functional Programs in F*
The functional core of F*
-
Recursive functions
val factorial : nat -> nat let rec factorial n = if n = 0 then 1 else n * (factorial (n - 1)) -
(Simple) inductive datatypes and pattern matching
type list (a:Type) = | Nil : list a | Cons : hd:a -> tl:list a -> list a let rec map (f:'a -> 'b) (x:list 'a) : list 'b = match x with | Nil -> Nil | Cons h t -> Cons (f h) (map f t) -
Lambda abstractions
map (fun x -> x + 42) [1;2;3]
Refinement types
type nat = x:int{x >= 0} (* general form x:t{phi x} *)-
Refinements introduced by type annotations (code unchanged)
val factorial : nat -> nat let rec factorial n = if n = 0 then 1 else n * (factorial (n - 1)) -
Logical obligations discharged by SMT (for else branch, simplified)
n >= 0, n <> 0 |= n - 1 >= 0 n >= 0, n <> 0, (factorial (n - 1)) >= 0 |= n * (factorial (n - 1)) >= 0 -
Refinements eliminated by subtyping:
nat <: intlet i : int = factorial 42 let f : x:nat{x > 0} -> int = factorial -
Refinement formulae (
phi) built from standard logical connectives=,<>,&&,||,not,...(bool-valued)==,=!=,/\,\/,~,forall,exists,...(prop-valued)
Dependent types
-
Dependent function types aka -types
val incr : x:int -> y:int{x < y} let incr x = x + 1 -
Can express pre- and postconditions of pure functions
val incr' : x:nat{odd x} -> y:nat{even y} -
Indexed inductive datatypes and implicit arguments (#-notation)
type vec (a:Type) : nat -> Type = | Nil : vec a 0 | Cons : #n:nat -> hd:a -> tl:vec a n -> vec a (n + 1) let rec map (#n:nat) (#a #b:Type) (f:a -> b) (as:vec a n) : vec b n = match as with | Nil -> Nil | Cons hd tl -> Cons (f hd) (map f tl)
Inductive families + refinement types
-
In Coq or Agda, we have to carry around explicit proofs, e.g.,
type vec (a:Type) : nat -> Type = | Nil : vec a 0 | Cons : #n:nat -> hd:a -> tl:vec a n -> vec a (n + 1) let rec lookup #a #n (as:vec a n) (i:nat) (p:i `less_than` n) : a = ... -
Combining
vecwith refinement types is much more convenientlet rec lookup #a #n (as:vec a n) (i:nat{i < n}) : a = match as with | Cons hd tl -> if i = 0 then hd else lookup tl (i - 1) -
Often even more convenient to use simple lists + refinement types
let rec length #a (as:list a) : nat = match as with | [] -> 0 | hd :: tl -> 1 + length tl let rec lookup #a (as:list a) (i:nat{i < (length as)}) : a = match as with | hd :: tl -> if i = 0 then hd else lookup tl (i - 1)
Total functions in F*
-
The F* functions we saw so far were all total
-
Toteffect (default) = no side-effects, terminates on all inputs(* val factorial : nat -> nat *) val factorial : nat -> Tot nat let rec factorial n = if n = 0 then 1 else n * (factorial (n - 1)) -
Quiz: How about giving this weaker type to factorial?
val factorial : int -> Tot int
let rec factorial n = if n = 0 then 1 else n * (factorial (n - 1))
^^^^^
Subtyping check failed; expected type (x:int{(x << n)}); got type int factorial (-1) loops! (int type in F* is unbounded)
The divergence effect (Dv)
-
We might not want to prove all code terminating
val factorial : int -> Dv int -
Some useful code really is not always terminating
- evaluator for lambda terms
val eval : exp -> Dv exp let rec eval e = match e with | App (Lam x e1) e2 -> eval (subst x e2 e1) | App e1 e2 -> eval (App (eval e1) e2) | Lam x e1 -> Lam x (eval e1) | _ -> e let main () = eval (App (Lam 0 (App (Var 0) (Var 0))) (Lam 0 (App (Var 0) (Var 0))))./Divergence.exe - servers
- …
- evaluator for lambda terms
Effect encapsulation (Tot and Dv)
-
Pure code cannot call potentially divergent code
-
Only (!) pure code can appear in specifications
val factorial : int -> Dv int type tau = x:int{x = factorial (-1)}type tau = x:int{x = factorial (-1)} ^^^^^^^^^^^^^^^^^^ Expected a pure expression; got an expression ... with effect "DIV" -
Sub-effecting:
Tot t <: Dv t -
So, divergent code can include pure code
incr 2 + factorial (-1) : Dv int
Tot and Dv are just two effects amongst many
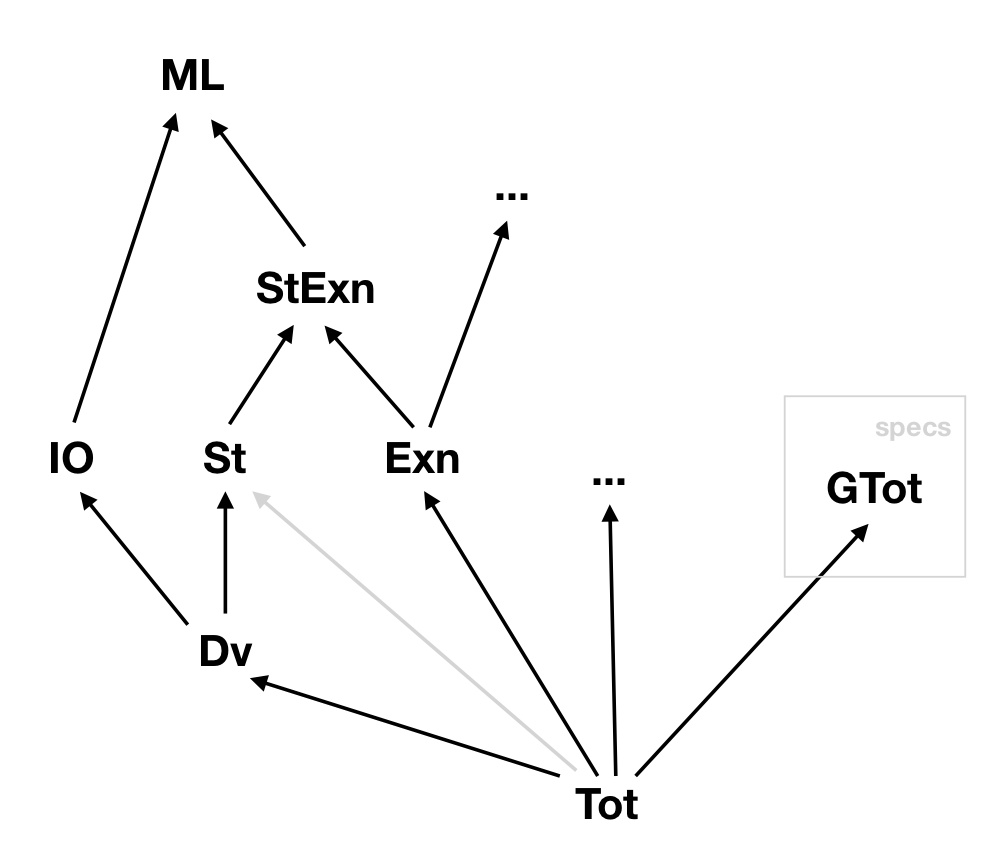
Effect encapsulation (Tot and GTot)
-
Ghost effect for code used only in specifications
val sel : #a:Type -> heap -> ref a -> GTot a -
Sub-effecting:
Tot t <: GTot t -
BUT NOT (!):
GTot t <: Tot t(holds for non-informative types) -
So, (informative) ghost code cannot be used in total functions
let f (g:unit -> GTot nat) : Tot (n:nat{n = g ()}) = g ()Computed type "n:nat{n = g ()}" and effect "GTot" is not compatible with the annotated type "n:nat{n = g ()}" effect "Tot" -
But total functions can appear in ghost code (regardless of their type)
let f (g:unit -> Tot nat) : GTot (n:nat{n = g ()}) = g ()
Verifying pure programs
Variant #1: intrinsically (at definition time)
- Using refinement types (saw this already)
val factorial : nat -> Tot nat (* type nat = x:int{x >= 0} *) - Can equivalently use pre- and postconditions for this
val factorial : x:int -> Pure int (requires (x >= 0)) (ensures (fun y -> y >= 0)) - Each F* computation type is of the form
- effect (e.g.
Pure) result type (e.g.int) spec. (e.g. pre and post)
- effect (e.g.
Totis just an abbreviationTot t = Pure t (requires True) (ensures (fun _ -> True))
Verifying pure programs
Variant #2: extrinsically using SMT-backed lemmas
let rec append (#a:Type) (xs ys:list a) : Tot (list a) =
match xs with
| [] -> ys
| x :: xs' -> x :: append xs' yslet rec lemma_append_length (#a:Type) (xs ys:list a)
: Pure unit
(requires True)
(ensures (fun _ -> length (append xs ys) = length xs + length ys)) =
match xs with
| [] -> ()
(* nil-VC: len (app [] ys) = len [] + len ys *)
| x :: xs' -> lemma_append_length xs' ys
(* len (app xs' ys) = len xs' + len ys *)
(* cons-VC: ==> len (app (x::xs') ys) = len (x::xs') + len ys *)- Convenient syntactic sugar: the
LemmaeffectLemma property = Pure unit (requires True) (ensures (fun _ -> property))
Often lemmas are unavoidable
let snoc l h = append l [h]
let rec rev #a (l:list a) : Tot (list a) =
match l with
| [] -> []
| hd::tl -> snoc (rev tl) hdval lemma_rev_snoc : #a:Type -> l:list a -> h:a ->
Lemma (rev (snoc l h) == h::rev l)
let rec lemma_rev_snoc (#a:Type) l h =
match l with
| [] -> ()
| hd::tl -> lemma_rev_snoc tl hval lemma_rev_involutive : #a:Type -> l:list a -> Lemma (rev (rev l) == l)
let rec lemma_rev_involutive (#a:Type) l =
match l with
| [] -> ()
| hd::tl -> lemma_rev_involutive tl; lemma_rev_snoc (rev tl) hdOften lemmas are unavoidable (but SMT can help)
let snoc l h = append l [h]
let rec rev #a (l:list a) : Tot (list a) =
match l with
| [] -> []
| hd::tl -> snoc (rev tl) hdval lemma_rev_snoc : #a:Type -> l:list a -> h:a ->
Lemma (rev (snoc l h) == h::rev l)
[SMTPat (rev (snoc l h))]
let rec lemma_rev_snoc (#a:Type) l h =
match l with
| [] -> ()
| hd::tl -> lemma_rev_snoc tl hval lemma_rev_involutive : #a:Type -> l:list a -> Lemma (rev (rev l) == l)
let rec lemma_rev_involutive (#a:Type) l =
match l with
| [] -> ()
| hd::tl -> lemma_rev_involutive tl (*; lemma_rev_snoc (rev tl) hd*)Verifying potentially divergent programs
The only variant: intrinsically (at definition time)
- Using refinement types
val factorial : nat -> Dv nat - Or the
Divcomputation type (pre- and postconditions)val eval_closed : e:exp -> Div exp (requires (closed e)) (ensures (fun e' -> Lam? e' /\ closed e')) let rec eval_closed e = match e with (* notice there is no match case for variables *) | App e1 e2 -> let Lam e1' = eval_closed e1 in below_subst_beta 0 e1' e2; eval_closed (subst (sub_beta e2) e1') | Lam e1 -> Lam e1 Dvis also just an abbreviationDv t = Div t (requires True) (ensures (fun _ -> True))
Recap: Functional core of F*
-
Variant of dependent type theory
- , , inductives, matches, universe polymorphism, …
-
General recursion and semantic termination check
- potential non-termination is an effect!
-
Refinements
- Refined value types:
x:t{phi x}
- Refined computation types:
Pure t pre postDiv t pre post
- refinements computationally and proof irrelevant, discharged by SMT
- Refined value types:
-
Subtyping and sub-effecting (
<:) -
Standard logical connectives (
==,/\,\/,forall,exists,...)
Verifying Stateful Programs in F*
Verifying stateful programs
-
The
Steffect—programming with garbage-collected referencesval incr : r:ref int -> St unit let incr r = r := !r + 1 -
Hoare logic-style preconditions and postconditions with
STval incr : r:ref int -> ST unit (requires (fun h0 -> True)) (ensures (fun h0 _ h2 -> sel h2 r == sel h0 r + 1 /\ modifies !{r} h0 h2))- precondition (requires) is a predicate on initial states
- postcondition (ensures) relates initial states, results, and final states
-
Stis again just an abbreviationSt t = ST t (requires True) (ensures (fun _ -> True)) -
Sub-effecting:
Pure <: STandDiv <: ST(partial correctness)
Heap and ST interfaces (much simplified)
module Heap
val heap : Type
val ref : Type -> Type
val sel : #a:Type -> heap -> ref a -> GTot a
val addr_of : #a:Type -> ref a -> GTot nat
val contains : #a:Type -> heap -> ref a -> Type0
let modifies (s:FStar.TSet.set nat) (h0 h1 : heap) =
forall a (r:ref a) . (h0 `contains` r /\ ~(addr_of r `mem` s))
==> sel h1 r == sel h0 rmodule ST
val alloc : #a:Type -> init:a ->
ST (ref a) (requires (fun _ -> True))
(ensures (fun h0 r h1 ->
modifies !{} h0 h1 /\ sel h1 r == init /\ fresh r h0 h1))
val (!) : #a:Type -> r:ref a ->
ST a (requires (fun _ -> True))
(ensures (fun h0 x h1 -> h0 == h1 /\ x == sel h0 r))
val (:=) : #a:Type -> r:ref a -> v:a ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\ sel h1 r == v))How does F* verify incr (intuition)
val incr : r:ref int ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h2 -> modifies !{r} h0 h2 /\
sel h2 r == sel h0 r + 1))let incr r = r := !r + 1- F*'s internal representation makes sequencing explicit
let incr r = let x = !r in r := x + 1
- F* uses the specs. of
!and:=to infer a specification forincrval incr : r:ref int -> ST unit (requires (fun _ -> True)) (ensures (fun h0 _ h2 -> exists h1 x. h0 == h1 /\ x == sel h0 r /\ //(!) modifies !{r} h1 h2 /\ sel h2 r == x + 1)) //(:=)
- SMT-solver checks if the inferred spec. implies the user-provided one
Typing rule for let / sequencing (intuition)
val incr : r:ref int ->
ST unit
(requires (fun _ -> True))
(ensures (fun h0 _ h2 ->
exists h1 x. h0 == h1 /\ x == sel h0 r /\ //(!)
modifies !{r} h1 h2 /\ sel h2 r == x + 1)) //(:=)
let incr r =
let x = !r in
r := x + 1
G |- e1 : ST t1 (requires (fun h0 -> pre))
(ensures (fun h0 x1 h1 -> post))
G, x1:t1 |- e2 : ST t2 (requires (fun h1 -> exists h0 . post))
(ensures (fun h1 x2 h2 -> post'))
---------------------------------------------------------------------------
G |- let x1 = e1 in e2 : ST t2 (requires (fun h0 -> pre))
(ensures (fun h x2 h2 ->
exists x1 h1 . post /\ post'))Reference swapping (hand proof sketch)
val swap : r1:ref int -> r2:ref int ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h3 -> modifies !{r1,r2} h0 h3 /\
sel h3 r2 == sel h0 r1 /\
sel h3 r1 == sel h0 r2))
let swap r1 r2 =
let t = !r1 in (* Know (P1) *)
r1 := !r2; (* Know (P2) *)
r2 := t (* Know (P3) *)(* (P1): exists h1 t. h0 == h1 /\ t == sel h0 r1 *)
(* (P2): exists h2. modifies !{r1} h1 h2 /\ sel h2 r1 == sel h1 r2 *)
(* (P3): modifies !{r2} h2 h3 /\ sel h3 r2 == t *)
(* `modifies !{r1,r2} h0 h3` follows directly from transitivity of modifies *)
(* `sel h3 r2 == sel h0 r1` follows immediately from (P1) and (P3) *)
(* Still to show: `sel h3 r1 == sel h0 r2`
From (P2) we know that `sel h2 r1 == sel h1 r2` (A)
From (P1) we know that h0 == h1
which directly gives us sel h1 r2 == sel h0 r2 (B)
From (P3) we know that modifies !{r2} h2 h3
which by definition gives us sel h2 r1 == sel h3 r1 (C)
We conclude by transitivity from (A)+(B)+(C) *)Integer reference swapping (the funny way)
val swap_add_sub : r1:ref int -> r2:ref int ->
ST unit (requires (fun _ -> addr_of r1 <> addr_of r2 ))
(ensures (fun h0 _ h1 -> modifies !{r1,r2} h0 h1 /\
sel h1 r1 == sel h0 r2 /\
sel h1 r2 == sel h0 r1))
let swap_add_sub r1 r2 =
r1 := !r1 + !r2;
r2 := !r1 - !r2;
r1 := !r1 - !r2-
Correctness of this variant relies on
r1andr2not being aliased -
… and on
intbeing unbounded (mathematical) integers
But you don't escape having to come up with invariants
Stateful Counting: 1 + 1 + 1 + 1 + 1 + 1 + …
let rec count_st_aux (r:ref nat) (n:nat)
: ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\
(* to ensure !{} in count_st *)
sel h1 r == sel h0 r + n
(* sel h1 r == n would be wrong *))) =
if n > 0 then (r := !r + 1;
count_st_aux r (n - 1))let rec count_st (n:nat)
: ST nat (requires (fun _ -> True))
(ensures (fun h0 x h1 -> modifies !{} h0 h1 /\
x == n)) =
let r = alloc 0 in
count_st_aux r n;
!r- You'll see more involved invariants in the lab exercises
Summary: Verifying Stateful Programs
-
ML-style garbage-collected references
val heap : Type val ref : Type -> Type val sel : #a:Type -> heap -> ref a -> GTot a val addr_of : #a:Type -> ref a -> GTot nat val modifies : s:set nat -> h0:heap -> h1:heap -> Type0 -
Steffect for simple ML-style programminglet incr (r:ref int) : St unit = r := !r + 1 -
STeffect for pre- and postcondition based (intrinsic) reasoningST unit (requires (fun h0 -> True)) (ensures (fun h0 _ h2 -> modifies !{r} h0 h2 /\ sel h2 r == n)) -
But that's not all there is to F*'s memory models!
- monotonicity, regions, heaps-and-stacks, resources and sep. logic
Highlights of Other F* Features
Low*: verifying low-level C code
Moto: The code (Low*) is low-level but the verification (F*) is not
let f (): Stack UInt64.t (requires (fun h0 -> True))
(ensures (fun h0 r h1 -> r = 43UL))
= push_frame (); (* pushing a new stack frame *)
let b = LowStar.Buffer.alloca 1UL 64ul in
assert (b.(42ul) = 1UL); (* high-level reasoning in F*'s logic *)
b.(42ul) <- b.(42ul) +^ 42UL;
let r = b.(42ul) in
pop_frame (); (* popping the stack frame we pushed above, *)
(* necessary for establishing Stack invariant *)
ruint64_t f()
{
uint64_t b[64U];
for (uint32_t _i = 0U; _i < (uint32_t)64U; ++_i)
b[_i] = (uint64_t)1U;
b[42U] = b[42U] + (uint64_t)42U;
uint64_t r = b[42U];
return r;
}F* has an extensible effect system
-
In addition to
Tot,St, …, users can define their own (monadic) effects -
Axiomatically (PLDI 2013)
- Only signatures of effect operations.
- Implementation in code extraction.
-
Dijkstra Monads For Free (POPL 2017)
- User provides a monadic effect definition
- F* then derives the effect and the specification calculus
-
Dijkstra Monads For All (ICFP 2019)
- User defines both the computational and specification monads.
- Comp. and spec. monads are related by effect observations.
-
Layered Effects (draft paper 2020)
- New effects on top of existing ones (like with monads in Haskell).
Meta-F* - a tactics and metaprogramming framework for F*
-
Tactics are just another F* effect (proof state + exceptions)
-
Can access the proof state, can introspect and synthesise F* terms
-
Run using the normalizer (slow) or compiled to native OCaml plugins
-
Uses: discharging VCs, massaging VCs, synthesizing terms, typeclasses
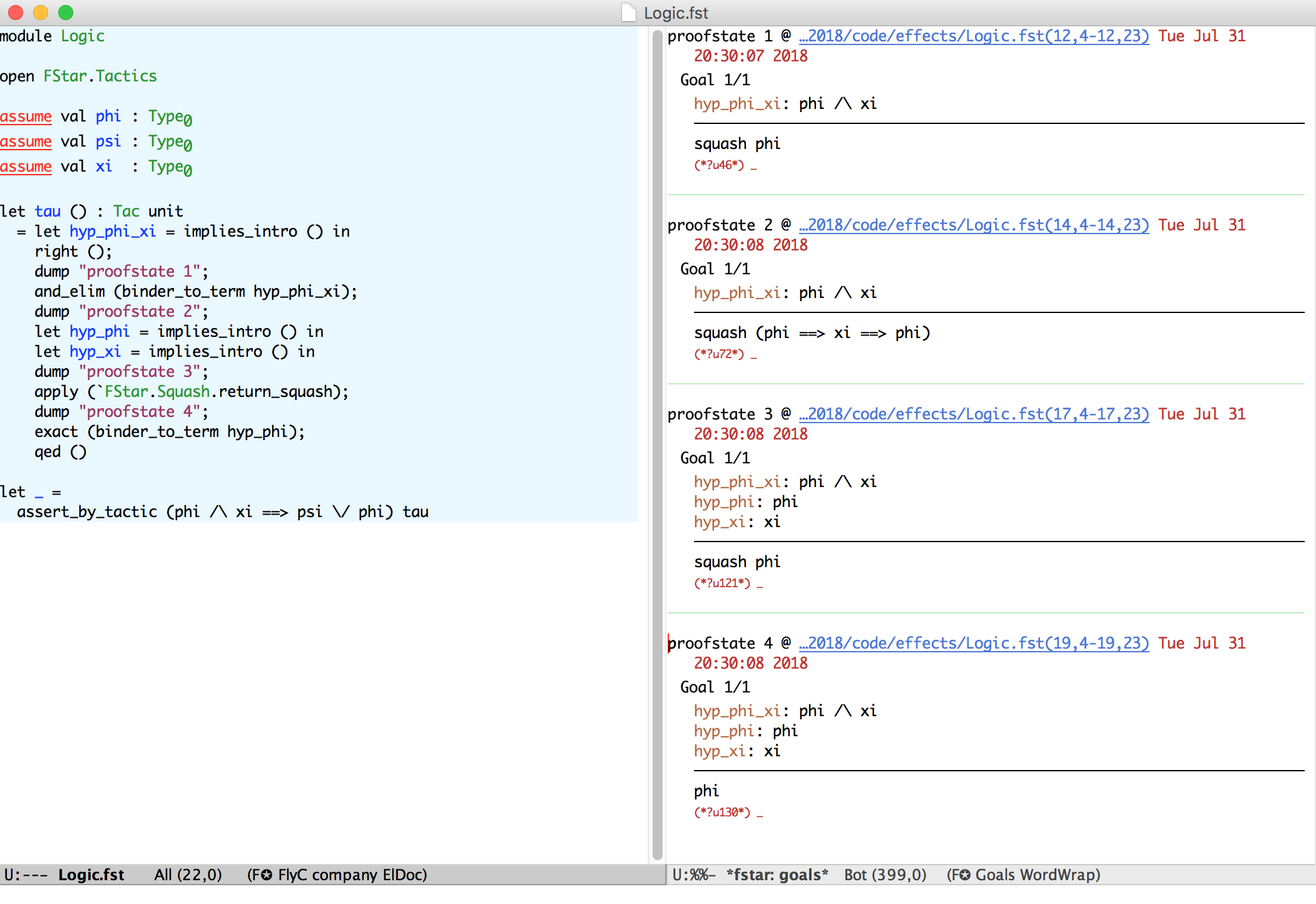
Tactics can discharge verification conditions (replacing SMT)
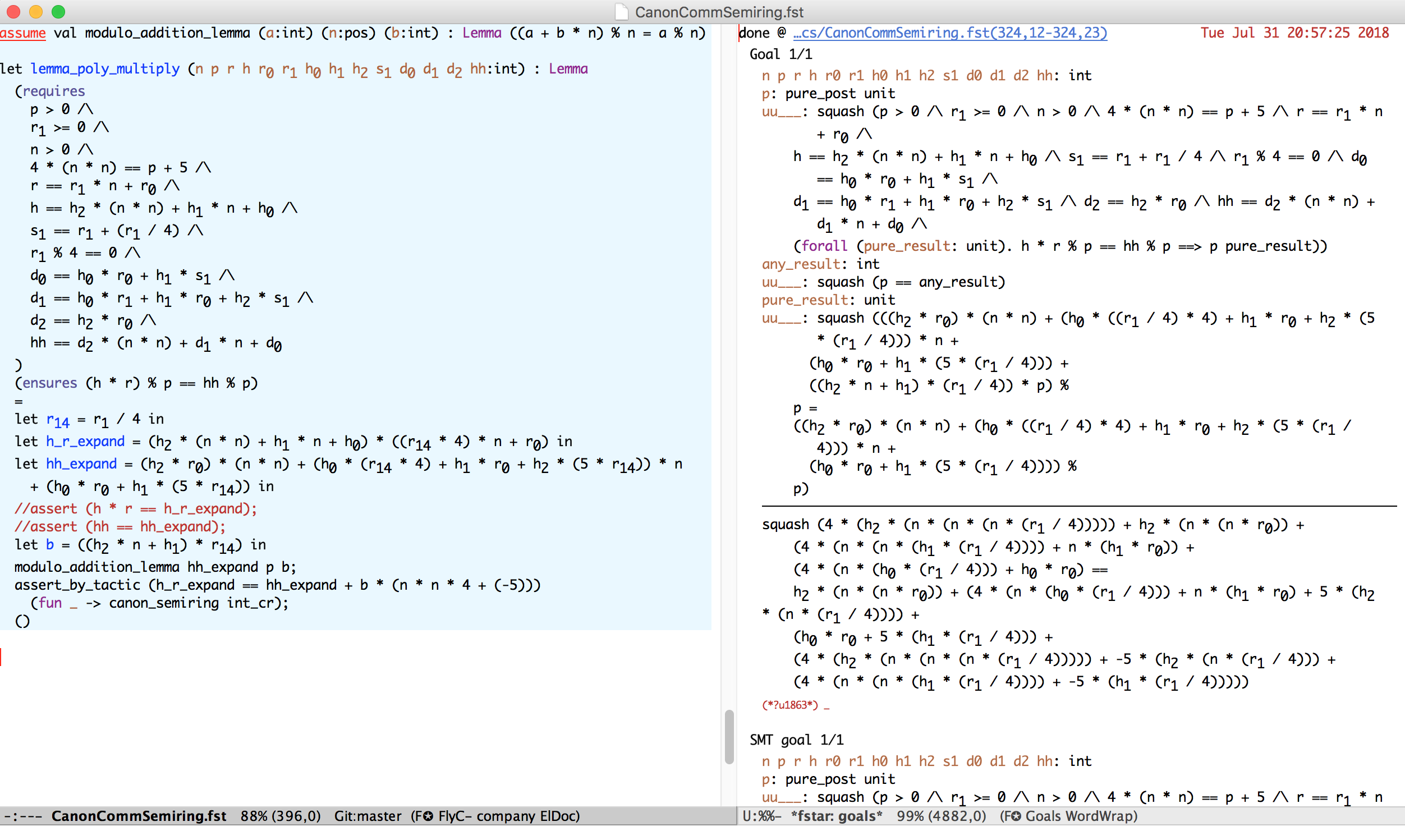
Tactics can massage verification conditions (complementing SMT)
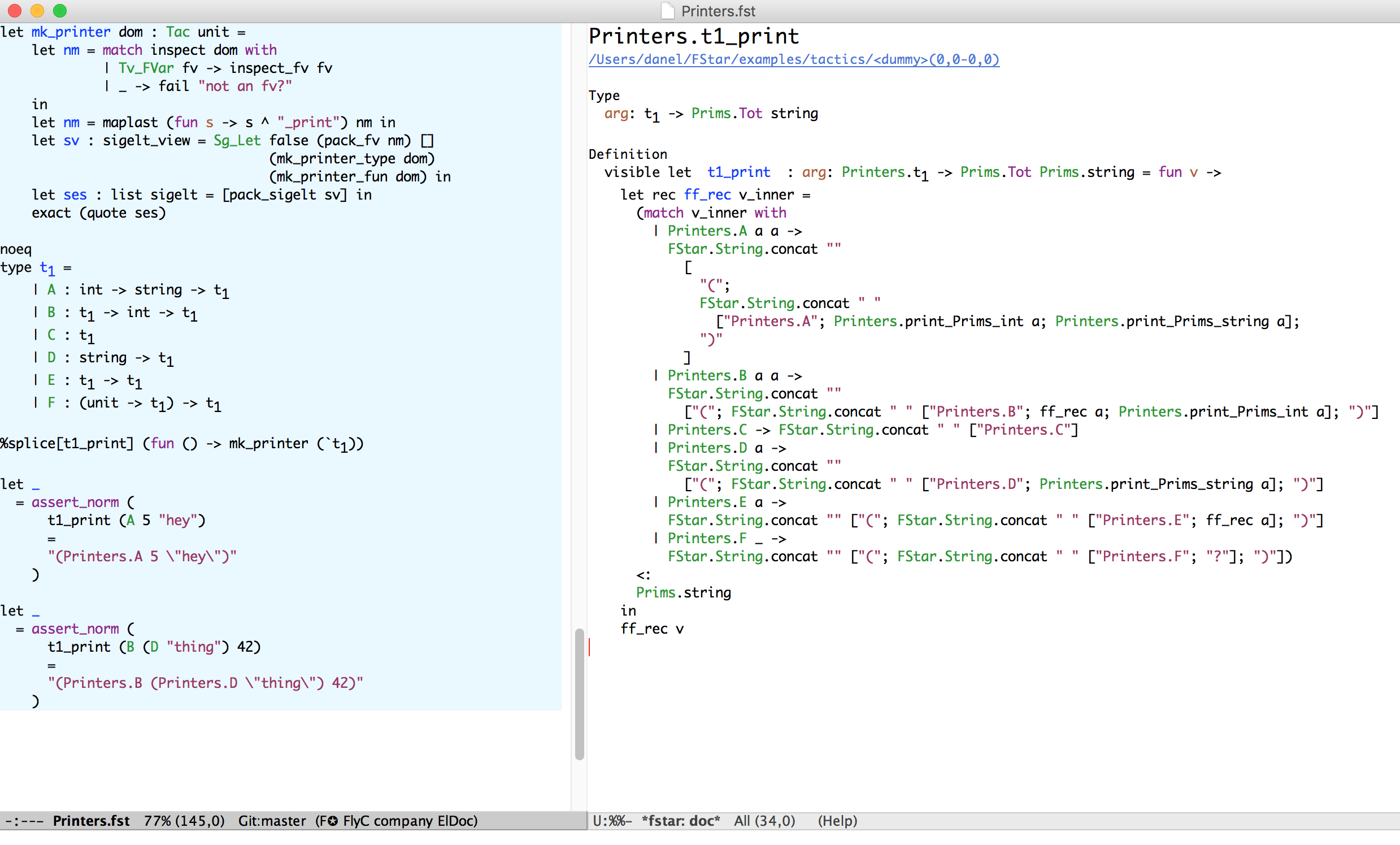
Tactics can synthesize F* terms (metaprogramming)
Tactics have also been used to extend F* with typeclasses
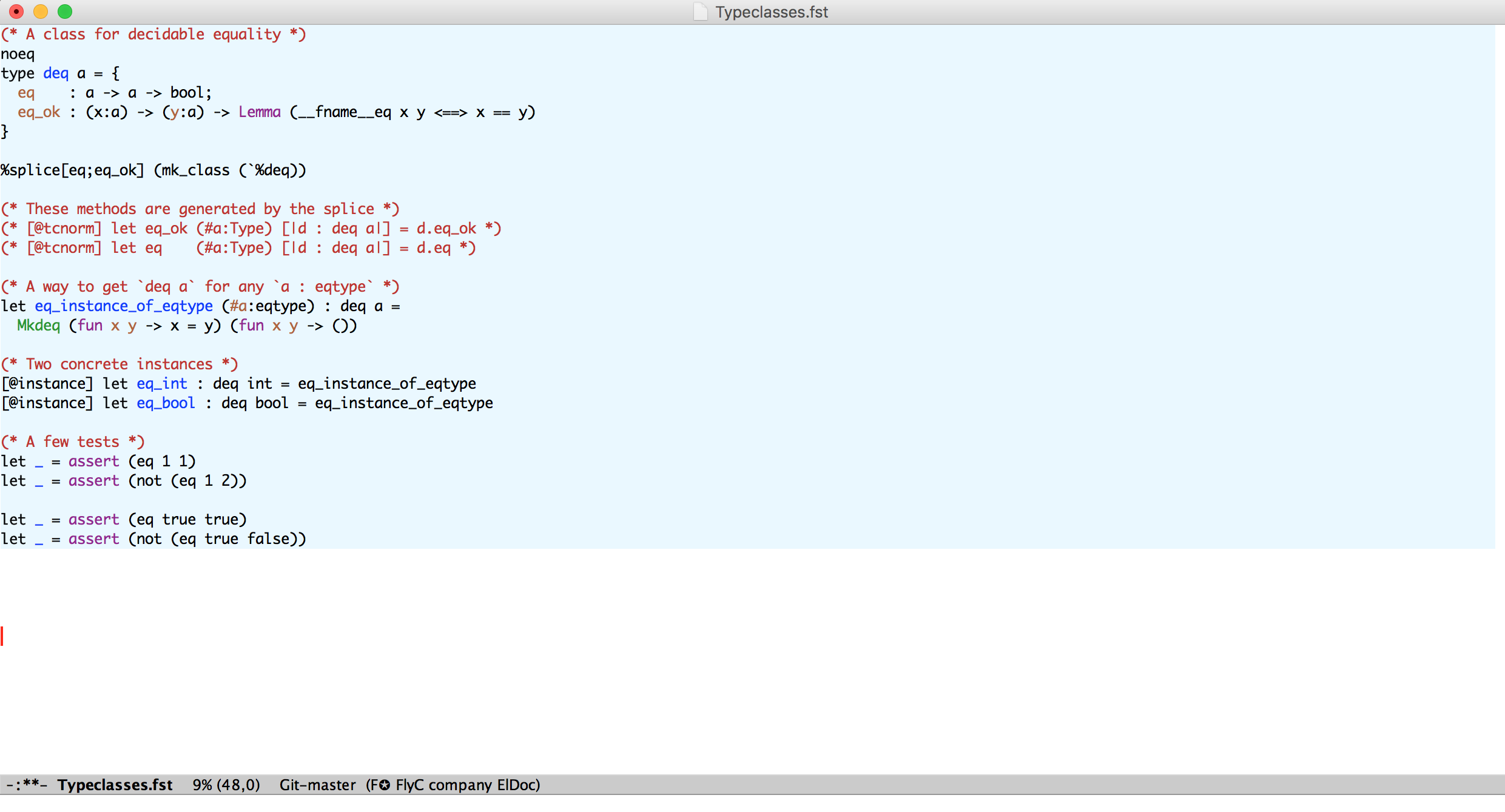
F*
-
An ML-style effectful functional programming language
-
A semi-automated SMT-based program verifier
-
An interactive dependently typed proof assistant
-
Used successfully in security and crypto verification
- Also applied to embedded IoT code (WIP with Juhan and Fabricio)
- If you would like to do a dissertation in this area, contact Juhan & me!
- If you would like to do a dissertation in this area, contact Juhan & me!
See you in the exercise class for a more hands-on experience with F*!
Bonus: Monotonic state
F*'s Memory Models are Based on Monotonicity
-
‘Containment for free’ for garbage collected references
val recall_contains #a (r:ref a) : ST unit (requires (fun _ -> True)) (ensures (fun h0 _ h1 -> h0 == h1 /\ h1 `contains` r)) -
val (!) : #a:Type -> r:ref a -> ST a (requires (fun _ -> True)) (ensures (fun h0 x h1 -> h0 == h1 /\ x == sel h0 r)) val (:=) : #a:Type -> r:ref a -> v:a -> ST unit (requires (fun _ -> True)) (ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\ sel h1 r == v)) -
Moreover,
ref ais actually amref a relwith a trivialrelval mref : a:Type -> rel:preorder a -> Type let ref a = mref a (fun _ _ -> True)
Monotonic References mref a rel
-
Such monotonic references also come with a modal operator
val token #a #rel (r:mref a rel) : (a -> Type0) -> Type0 -
And corresponding introduction and elimination rules (stateful progs.)
val witness_token #a #rel (r:mref a rel) (p:(a -> Type0)) : ST unit (requires (fun h0 -> p (sel h0 r) /\ stable p rel)) (ensures (fun h0 _ h1 -> h0 == h1 /\ token r p)) val recall_token #a #rel (r:mref a rel) (p:(a -> Type0)) : ST unit (requires (fun _ -> token r p)) (ensures (fun h0 _ h1 -> h0 == h1 /\ p (sel h1 r))) -
Enabling the following useful verification pattern
let p (x:nat) = x > 0 in (* assuming (r : mref nat `<=`) *) r := !r + 1; witness r p; black_box r; recall r p; assert (p !r) -
Examples: counters, logs, network traffic history, state continuity, …
