Program Verification with F*
Overview
-
What is F*?
-
Verifying Purely Functional Programs in F*
-
Verifying Effectful Programs in F* (Div, State, IO, Exc, ND, …)
-
Highlights of Other F* Features
Tutorials, research papers, past courses and talks, setup instructions
@
https://www.fstar-lang.org/
Do ask questions!
What is F*?
Program verification: Shall the twain ever meet?
| Interactive proof assistants | Semi-automated verifiers of imperative programs | |||
|---|---|---|---|---|
| Coq, | air | Dafny, | ||
| Agda, | FramaC, | |||
| Lean, | gap | Why3, | ||
| Isabelle | Liquid Haskell | |||
-
Left side: very expressive logics, interactive proving, tactics
- but mostly only purely functional programming
- but mostly only purely functional programming
-
Right side: effectful programming, SMT-based automation
- but only very weak logics
Bridging the air gap: F*
- Functional programming language with effects
-
like F#, OCaml, Haskell, …
let incr = fun (r:ref a) -> r := !r + 1but with a much richer type system
-
by default extracted to OCaml or F#
-
subset extracted to efficient C code (Low* and KreMLin)
-
- Semi-automated verification system using SMT (Z3)
- push-button automation like in Dafny, FramaC, Why3, Liquid Haskell, …
- Interactive proof assistant based on dependent types
- interactive proving and tactics like in Coq, Agda, Lean, …
F* in action, at scale
-
Functional programming language with effects
- F* is programmed in F*, but not (yet) verified
-
Semi-automated verification system
- Project Everest: verify and deploy new, efficient HTTPS stack
-
Proof assistant based on dependent types
- Fallback when SMT fails; also for mechanized metatheory
- MicroFStar: Fragment of F* formalized in F*
- Wys*: Verified DSL for secure multi-party computations
- ReVerC: Verified compiler to reversible circuits
- Meta-F* (metaprogramming and tactics) increasingly used in Everest
- Fallback when SMT fails; also for mechanized metatheory
The current F* team
Microsoft Research (US, UK, India), Inria Paris, MIT, Rosario, …
| Danel Ahman Benjamin Beurdouche Karthikeyan Bhargavan Barry Bond Antoine Delignat-Lavaud Victor Dumitrescu Cédric Fournet Chris Hawblitzel Cătălin Hriţcu Markulf Kohlweiss Qunyan Mangus Kenji Maillard | Asher Manning Guido Martínez Zoe Paraskevopoulou Clément Pit-Claudel Jonathan Protzenko Tahina Ramananandro Aseem Rastogi Nikhil Swamy (benevolent dictator) Christoph M. Wintersteiger Santiago Zanella-Béguelin Gustavo Varo | |
How to use F*
-
Two kinds of F* files
-
A.fsti - interface file for module called A (can be omitted)
-
A.fst - source code file for module called A
-
- Command line: typechecking/verification
$ fstar.exe Ackermann.fst
Verified module: Ackermann (429 milliseconds)
All verification conditions discharged successfully- Command line: typechecking/verification + program extraction
$ fstar.exe Ackermann.fst --odir out-dir --codegen OCaml- Interactive: development + verification (Emacs with fstar-mode)
Verifying Purely Functional Programs in F*
The functional core of F*
-
Recursive functions
val factorial : nat -> nat let rec factorial n = if n = 0 then 1 else n * (factorial (n - 1)) -
(Simple) inductive datatypes and pattern matching
type list (a:Type) = | Nil : list a | Cons : hd:a -> tl:list a -> list a let rec map (f:'a -> 'b) (x:list 'a) : list 'b = match x with | Nil -> Nil | Cons h t -> Cons (f h) (map f t) -
Lambdas
map (fun x -> x + 42) [1;2;3]
Refinement types
type nat = x:int{x >= 0} (* general form x:t{phi x} *)-
Refinements introduced by type annotations (code unchanged)
val factorial : nat -> nat let rec factorial n = if n = 0 then 1 else (n * factorial (n - 1)) -
Logical obligations discharged by SMT (for else branch, simplified)
n >= 0, n <> 0 |= n - 1 >= 0 n >= 0, n <> 0, (factorial (n - 1)) >= 0 |= (n * factorial (n - 1)) >= 0 -
Refinements eliminated by subtyping:
nat <: intlet i : int = factorial 42 -
Logic in refinement types
-
=,<>,&&,||,not(bool-valued) -
==,=!=,/\,\/,~,forall,exists(prop-valued)
-
Dependent types
-
Dependent function types aka -types
val incr : x:int -> y:int{x < y} let incr x = x + 1 -
Can express pre- and postconditions of pure functions
val incr' : x:nat{odd x} -> y:nat{even y} -
(Parameterised and indexed) inductive datatypes; implicit arguments
type vec (a:Type) : nat -> Type = | Nil : vec a 0 | Cons : #n:nat -> hd:a -> tl:vec a n -> vec a (n + 1) let rec map (#n:nat) (#a #b:Type) (f:a -> b) (as:vec a n) : vec b n = match as with | Nil -> Nil | Cons hd tl -> Cons (f hd) (map f tl)
Inductive families + refinement types
-
As in Coq or Agda, we could type and define the lookup function as
type vec (a:Type) : nat -> Type = | Nil : vec a 0 | Cons : #n:nat -> hd:a -> tl:vec a n -> vec a (n + 1) let rec lookup #a #n (as:vec a n) (i:nat) (p:i `less_than` n) : a = ... -
But combining
vecwith refinement types is much more convenientlet rec lookup #a #n (as:vec a n) (i:nat{i < n}) : a = match as with | Cons hd tl -> if i = 0 then hd else (lookup tl (i - 1)) -
Often even more convenient to use simple lists + refinement types
let rec length #a (as:list a) : nat = match as with | [] -> 0 | hd :: tl -> 1 + length tl let rec lookup #a (as:list a) (i:nat{i < (length as)}) : a = match as with | hd :: tl -> if i = 0 then hd else (lookup tl (i - 1))
Total functions in F*
-
The F* functions we saw so far were all total
-
Toteffect (default) = no side-effects, terminates on all inputs(* val factorial : nat -> nat *) val factorial : nat -> Tot nat let rec factorial n = if n = 0 then 1 else n * (factorial (n - 1)) -
Quiz: How about giving this weaker type to factorial?
val factorial : int -> Tot int
let rec factorial n = if n = 0 then 1 else n * (factorial (n - 1))
^^^^^
Subtyping check failed; expected type (x:int{(x << n)}); got type int factorial (-1) loops! (int type in F* is unbounded)
The divergence effect (Dv)
-
We might not want to prove all code terminating
val factorial : int -> Dv int -
Some useful code really is not always terminating
- evaluator for lambda terms
val eval : exp -> Dv exp let rec eval e = match e with | App (Lam x e1) e2 -> eval (subst x e2 e1) | App e1 e2 -> eval (App (eval e1) e2) | Lam x e1 -> Lam x (eval e1) | _ -> e let main () = eval (App (Lam 0 (App (Var 0) (Var 0))) (Lam 0 (App (Var 0) (Var 0))))./Divergence.exe - servers
- …
- evaluator for lambda terms
Effect encapsulation (Tot and Dv)
-
Pure code cannot call potentially divergent code
-
Only (!) pure code can appear in specifications
val factorial : int -> Dv int type tau = x:int{x = factorial (-1)}type tau = x:int{x = factorial (-1)} ^^^^^^^^^^^^^^^^^^ Expected a pure expression; got an expression ... with effect "DIV" -
Sub-effecting:
Tot t <: Dv t -
So, divergent code can include pure code
incr 2 + factorial (-1) : Dv int
Effect encapsulation (Tot and GTot)
-
Ghost effect for code used only in specifications
val sel : #a:Type -> heap -> ref a -> GTot a val incr : r:ref int -> ST unit (requires (fun h0 -> True)) (ensures (fun h0 _ h2 -> sel h2 r == sel h0 r + 1)) -
Sub-effecting:
Tot t <: GTot t -
BUT NOT (!):
GTot t <: Tot t(holds for non-informative types)
Verifying pure programs
Variant #1: intrinsically (at definition time)
- Using refinement types (saw this already)
val factorial : nat -> Tot nat (* type nat = x:int{x >= 0} *) - Can equivalently use pre- and postconditions for this
val factorial : x:int -> Pure int (requires (x >= 0)) (ensures (fun y -> y >= 0)) - Each F* computation type is of the form
- effect (e.g.
Pure) result type (e.g.int) spec. (e.g. pre and post)
- effect (e.g.
Totis just an abbreviationTot t = Pure t (requires True) (ensures (fun _ -> True))
Verifying pure programs
Variant #2: extrinsically using SMT-backed lemmas
let rec append (#a:Type) (xs ys:list a) : Tot (list a) =
match xs with
| [] -> ys
| x :: xs' -> x :: append xs' yslet rec lemma_append_length (#a:Type) (xs ys:list a)
: Pure unit
(requires True)
(ensures (fun _ -> length (append xs ys) = length xs + length ys)) =
match xs with
| [] -> ()
(* nil-VC: len (app [] ys) = len [] + len ys *)
| x :: xs' -> lemma_append_length xs' ys
(* len (app xs' ys) = len xs' + len ys *)
(* cons-VC: ==> len (app (x::xs') ys) = len (x::xs') + len ys *)- Convenient syntactic sugar: the
LemmaeffectLemma (property) = Pure unit (requires True) (ensures (fun _ -> property))
Often lemmas are unavoidable
let snoc l h = append l [h]
let rec rev #a (l:list a) : Tot (list a) =
match l with
| [] -> []
| hd::tl -> snoc (rev tl) hdval lemma_rev_snoc : #a:Type -> l:list a -> h:a ->
Lemma (rev (snoc l h) == h::rev l)
let rec lemma_rev_snoc #a l h =
match l with
| [] -> ()
| hd::tl -> lemma_rev_snoc tl hval lemma_rev_involutive : #a:Type -> l:list a -> Lemma (rev (rev l) == l)
let rec lemma_rev_involutive #a l =
match l with
| [] -> ()
| hd::tl -> lemma_rev_involutive tl; lemma_rev_snoc (rev tl) hdOften lemmas are unavoidable (but SMT can help)
let snoc l h = append l [h]
let rec rev #a (l:list a) : Tot (list a) =
match l with
| [] -> []
| hd::tl -> snoc (rev tl) hdval lemma_rev_snoc : #a:Type -> l:list a -> h:a ->
Lemma (rev (snoc l h) == h::rev l)
[SMTPat (rev (snoc l h))]
let rec lemma_rev_snoc #a l h =
match l with
| [] -> ()
| hd::tl -> lemma_rev_snoc tl hval lemma_rev_involutive : #a:Type -> l:list a -> Lemma (rev (rev l) == l)
let rec lemma_rev_involutive #a l =
match l with
| [] -> ()
| hd::tl -> lemma_rev_involutive tl (*; lemma_rev_snoc (rev tl) hd*)Verifying potentially divergent programs
The only variant: intrinsically (partial correctness)
- Using refinement types
val factorial : nat -> Dv nat - Or the
Divcomputation type (pre- and postconditions)val eval_closed : e:exp -> Div exp (requires (closed e)) (ensures (fun e' -> Lam? e' /\ closed e')) let rec eval_closed e = match e with (* notice there is no match case for variables *) | App e1 e2 -> let Lam e1' = eval_closed e1 in below_subst_beta 0 e1' e2; eval_closed (subst (sub_beta e2) e1') | Lam e1 -> Lam e1 Dvis also just an abbreviationDv t = Div t (requires True) (ensures (fun _ -> True))
Recap: Functional core of F*
-
Variant of dependent type theory
- , , inductives, matches, universe polymorphism
-
General recursion and semantic termination check
- potential non-termination is an effect
-
Refinements
- Refined value types:
x:t{p}
- Refined computation types:
Pure t pre postDiv t pre post
- refinements computationally and proof irrelevant, discharged by SMT
- Refined value types:
-
Subtyping and sub-effecting (
<:) -
Different kinds of logical connectives (
=,&&,||, …) vs (==,/\,\/, …)
Verifying Stateful Programs in F*
Verifying stateful programs
-
The
Steffect—programming with garbage-collected referencesval incr : r:ref int -> St unit let incr r = r := !r + 1 -
Hoare logic-style preconditions and postconditions with
STval incr : r:ref int -> ST unit (requires (fun h0 -> True)) (ensures (fun h0 _ h2 -> modifies !{r} h0 h2 /\ sel h2 r == sel h0 r + 1))- precondition (requires) is a predicate on initial states
- postcondition (ensures) relates initial states, results, and final states
-
Stis again just an abbreviationSt t = ST t (requires (fun _ -> True)) (ensures (fun _ _ _ -> True)) -
Sub-effecting:
Pure <: STandDiv <: ST(partial correctness)
Heap and ST interfaces (much simplified)
val heap : Type (* heap = c:nat & h:(nat -> option (a:Type & a)){...}*)
val ref : Type -> Type
val sel : #a:Type -> heap -> ref a -> GTot a (* plus eq lemmas *)
val upd : #a:Type -> heap -> ref a -> a -> GTot heap
val contains : #a:Type -> heap -> ref a -> Type
val modifies : set nat -> heap -> heap -> Typeval alloc : #a:Type -> init:a ->
ST (ref a) (requires (fun _ -> True))
(ensures (fun h0 r h1 ->
modifies !{} h0 h1 /\ sel h1 r == init /\ fresh r h0 h1))
val (!) : #a:Type -> r:ref a ->
ST a (requires (fun _ -> True))
(ensures (fun h0 x h1 -> h0 == h1 /\ x == sel h0 r))
val (:=) : #a:Type -> r:ref a -> v:a ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\ sel h1 r == v))val recall : #a:Type -> r:ref a ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h1 -> h0 == h1 /\ h1 `contains` r))Verifying incr (intuition)
let incr r = r := !r + 1val incr : r:ref int ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h2 -> modifies !{r} h0 h2 /\
sel h2 r == sel h0 r + 1))val incr : r:ref int ->
ST unit
(requires (fun _ -> True))
(ensures (fun h0 _ h2 ->
exists h1 x. h0 == h1 /\ x == sel h0 r /\ //(!)
modifies !{r} h1 h2 /\ sel h2 r == x+1)) //(:=)
let incr r =
let x = !r in
r := x + 1val (!) : #a:Type -> r:ref a ->
ST a (requires (fun _ -> True))
(ensures (fun h0 x h1 -> h0 == h1 /\ x == sel h0 r))
val (:=) : #a:Type -> r:ref a -> v:a ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\ sel h1 r == v))Typing rule for let / sequencing (intuition)
val incr : r:ref int ->
ST unit
(requires (fun _ -> True))
(ensures (fun h0 _ h2 ->
exists h1 x. h0 == h1 /\ x == sel h0 r /\ //(!)
modifies !{r} h1 h2 /\ sel h2 r == x+1)) //(:=)
let incr r =
let x = !r in
r := x + 1
G |- e1 : ST t1 (requires (fun h0 -> pre))
(ensures (fun h0 x1 h1 -> post))
G, x1:t1 |- e2 : ST t2 (requires (fun h1 -> exists h0 . post))
(ensures (fun h1 x2 h2 -> post'))
---------------------------------------------------------------------------
G |- let x1 = e1 in e2 : ST t2 (requires (fun h0 -> pre))
(ensures (fun h x2 h2 ->
exists x1 h1 . post /\ post'))Reference swapping (two ways)
val swap : r1:ref int -> r2:ref int ->
ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h3 -> modifies !{r1,r2} h0 h3 /\
sel h3 r2 == sel h0 r1 /\
sel h3 r1 == sel h0 r2))
let swap r1 r2 =
let t = !r1 in
r1 := !r2;
r2 := tval swap_add_sub : r1:ref int -> r2:ref int ->
ST unit (requires (fun _ -> addr_of r1 <> addr_of r2 ))
(ensures (fun h0 _ h1 -> modifies !{r1,r2} h0 h1 /\
sel h1 r1 == sel h0 r2 /\
sel h1 r2 == sel h0 r1))
let swap_add_sub r1 r2 =
r1 := !r1 + !r2;
r2 := !r1 - !r2;
r1 := !r1 - !r2But you don't escape having to come up with invariants
Stateful Count: 1 + 1 + 1 + 1 + 1 + 1 + …
let rec count_st_aux (r:ref nat) (n:nat)
: ST unit (requires (fun _ -> True))
(ensures (fun h0 _ h1 -> modifies !{r} h0 h1 /\
(* to ensure !{} in count_st *)
sel h1 r == sel h0 r + n
(* sel h1 r == n would be wrong *))) =
if n > 0 then (r := !r + 1;
count_st_aux r (n - 1))let rec count_st (n:nat)
: ST nat (requires (fun _ -> True))
(ensures (fun h0 x h1 -> modifies !{} h0 h1 /\ x == n)) =
let r = alloc 0 in
count_st_aux r n;
!r- See past F* courses for examples with more involved invariants
But you don't escape having to come up with invariants ctd
Stateful Fibonacci: 1 , 1 , 2 , 3 , 5 , 8 , …
let rec fibonacci (n:nat) : GTot nat
= if n <= 1 then 1 else fibonacci (n - 1) + fibonacci (n - 2)let rec fibonacci_aux (i:pos) (n:nat{n >= i}) (r1 r2:ref nat)
: ST unit (requires (fun h0 -> addr_of r1 <> addr_of r2 /\
sel h0 r1 = fibonacci (i - 1) /\
sel h0 r2 = fibonacci i ))
(ensures (fun h0 a h1 -> sel h1 r1 = fibonacci (n - 1) /\
sel h1 r2 = fibonacci n /\
modifies !{r1,r2} h0 h1))
= if i < n then
(let temp = !r2 in
r2 := !r1 + !r2; (* fib (i+1) = fib i + fib (i-1) *)
r1 := temp; (* fib i we already have *)
fibonacci_aux (i+1) n r1 r2) (* tail-recursion *)let fibonacci_st (n:nat)
: ST nat (requires (fun _ -> True))
(ensures (fun h0 x h1 -> modifies !{} h0 h1 /\
x = fibonacci n))
= if n <= 1 then 1
else (let (r1,r2) = (alloc 1,alloc 1) in
fibonacci_aux 1 n r1 r2;
!r2)Summary: Verifying Stateful Programs
-
ML-style garbage-collected references
val heap : Type val ref : Type -> Type val sel : #a:Type -> heap -> ref a -> GTot a val upd : #a:Type -> heap -> ref a -> a -> GTot heap val modifies : set nat -> heap -> heap -> Type -
Steffect for simple ML-style programminglet incr (r:ref int) : St unit = r := !r + 1 -
STeffect for pre- and postcondition based (intrinsic) reasoningST unit (requires (fun h0 -> True)) (ensures (fun h0 _ h2 -> modifies !{r} h0 h2 /\ sel h2 r == n)) -
But that's not all there is to F*'s memory models!
- monotonicity, regions, heaps-and-stacks (for low-level programming)
Verifying Programs with Other Effects in F*
Other Effects in F*
-
Dijkstra Monads for Free (POPL 2017)
-
Given a mon. definition, F* derives the effect and the spec. calculus
-
Spec. calc. is a monad of (Dijkstra's) predicate transformers
-
ST a pre post = STATE a (wp_pre_post : st_spec a)
-
-
Supports Reader, Writer, State, Exceptions, but not (!) nondet. and IO
val throw : #a:Type -> e:exn -> Exc a (requires (True)) (ensures (fun (r:either a exn) -> r = inr e))
-
Also comes with monadic reification for extrinsic reasoning
val reify : St a -> (int -> a * int) (* much simplified signature *) let incr (n:N) : St unit = put (get() + n) let incr2 (h:bool) : St unit = if h then (incr 2) else (incr 1; incr 1) assert (forall h0 h1 l. reify (incr2 h0) l = reify (incr2 h1) l) (* NI *)
- CPP 2018: Relational reasoning in F* (IFC & NI, crypto proofs, …)
-
Other Effects in F* ctd
-
Dijkstra Monads for All (Under review, 2019)
-
No more (!) attempting to pair a comp. monad with a single spec.
-
Dijksta monads (e.g.,
ST) now flexibly defined from-
computational monad
(M)and specification monad(W) -
monad morphism / monadic relation
(M -> W)
-
-
As a result, F* now also supports nondeterminism and IO
let do_io_then_roll_back_state () : IOST unit (requires (fun s h -> True)) (* state + IO effect *) (ensures (fun s h r s' l -> s = s' /\ (exists i . l = [In i; Out (s + i + 1)]))) = let s = get () in let i = read () in put (s + i); (* some other observably pure computation *) let s' = get () in write (s' + 1); put s
-
Highlights of Other F* Features
Highlights of Other F* Features
-
Low*: programming and verifying low-level C code (ICFP 2017)
-
Idea: The code (Low*) is low-level but the verification (F*) is not
-
Uses a hierarchical region-based heap-and-stack memory model
-
-
F* has good support for monotonic state (POPL 2018)
-
Global state where writes have to follow a preorder (an upd. monad)
-
Combines pre-postconditions based verification with modal logic
-
Basis of F* memory models (GCd refs, GCd mrefs, dealloc refs, Low*, …)
-
-
Meta-F* - a tactics and metaprogramming framework (ESOP 2019)
-
Tactics are just another F* effect (proof state + exceptions)
-
Ran using the normalizer (slow) or compiled to native OCaml plugins
-
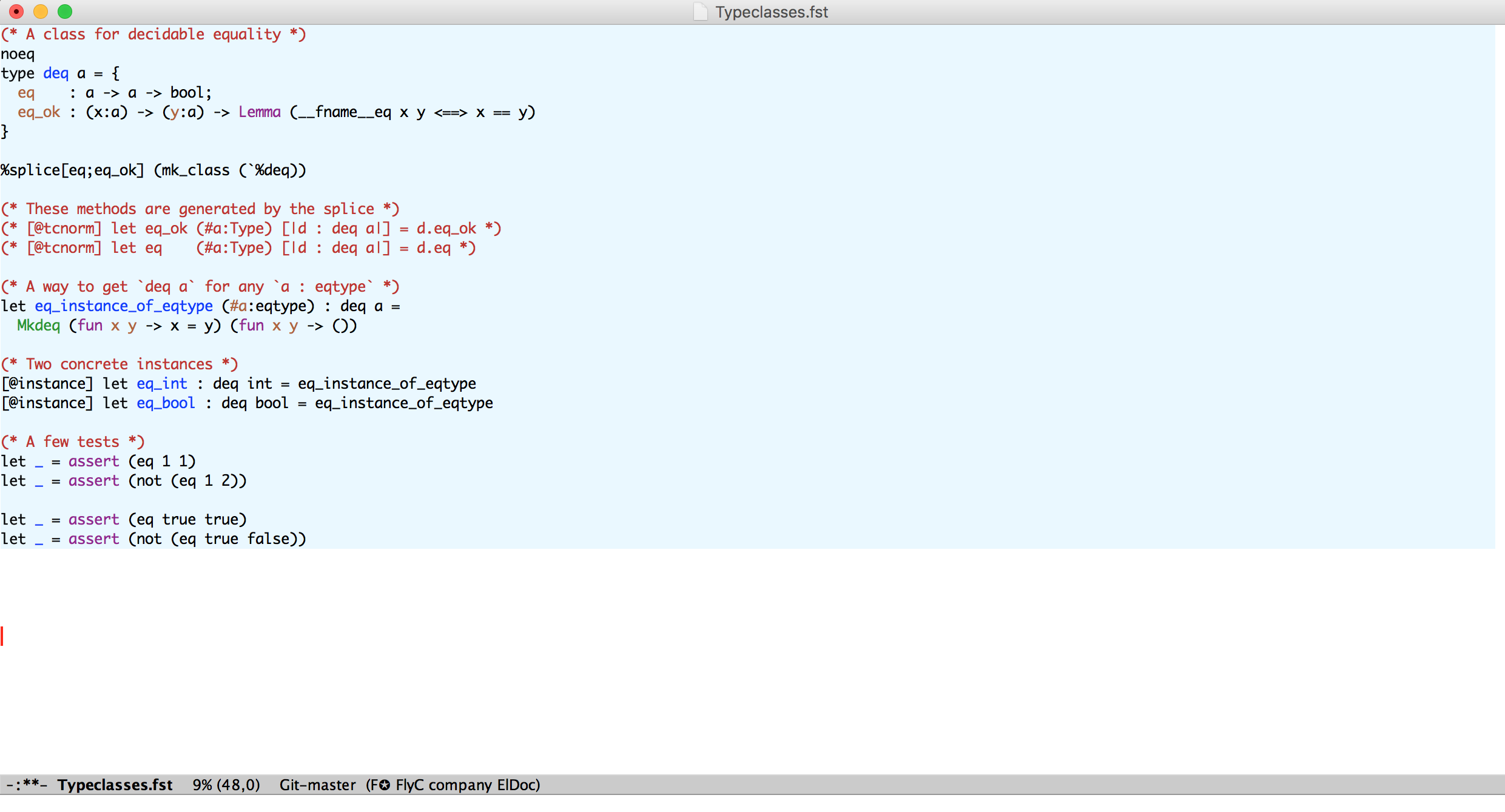
Uses: discharging VCs, massaging VCs, synthesizing terms, typeclasses
-
F*
-
An ML-style effectful functional programming language
-
A semi-automated SMT-based program verifier
-
An interactive dependently typed proof assistant
-
Used successfully in security and crypto verification
-
miTLS: F*-verified reference implementation of TLS
-
HACL*: F*-verified crypto (used in Firefox and Wireguard)
-
Vale: F*-verified assembly language (POPL 2019)
-
Low*: a small example
let f (): Stack UInt64.t (requires (fun _ -> True))
(ensures (fun _ _ _ -> True))
= push_frame (); (* pushing a new stack frame *)
let b = LowStar.Buffer.alloca 1UL 64ul in
assert (b.(42ul) = 1UL); (* high-level reasoning in F*'s logic *)
b.(42ul) <- b.(42ul) +^ 42UL;
let r = b.(42ul) in
pop_frame (); (* popping the stack frame we pushed above *)
(* necessary for establishing Stack invariant *)
assert (r = 43UL);
ruint64_t f()
{
uint64_t b[64U];
for (uint32_t _i = 0U; _i < (uint32_t)64U; ++_i)
b[_i] = (uint64_t)1U;
b[42U] = b[42U] + (uint64_t)42U;
uint64_t r = b[42U];
return r;
}Tactics can discharge verification conditions (replacing SMT)
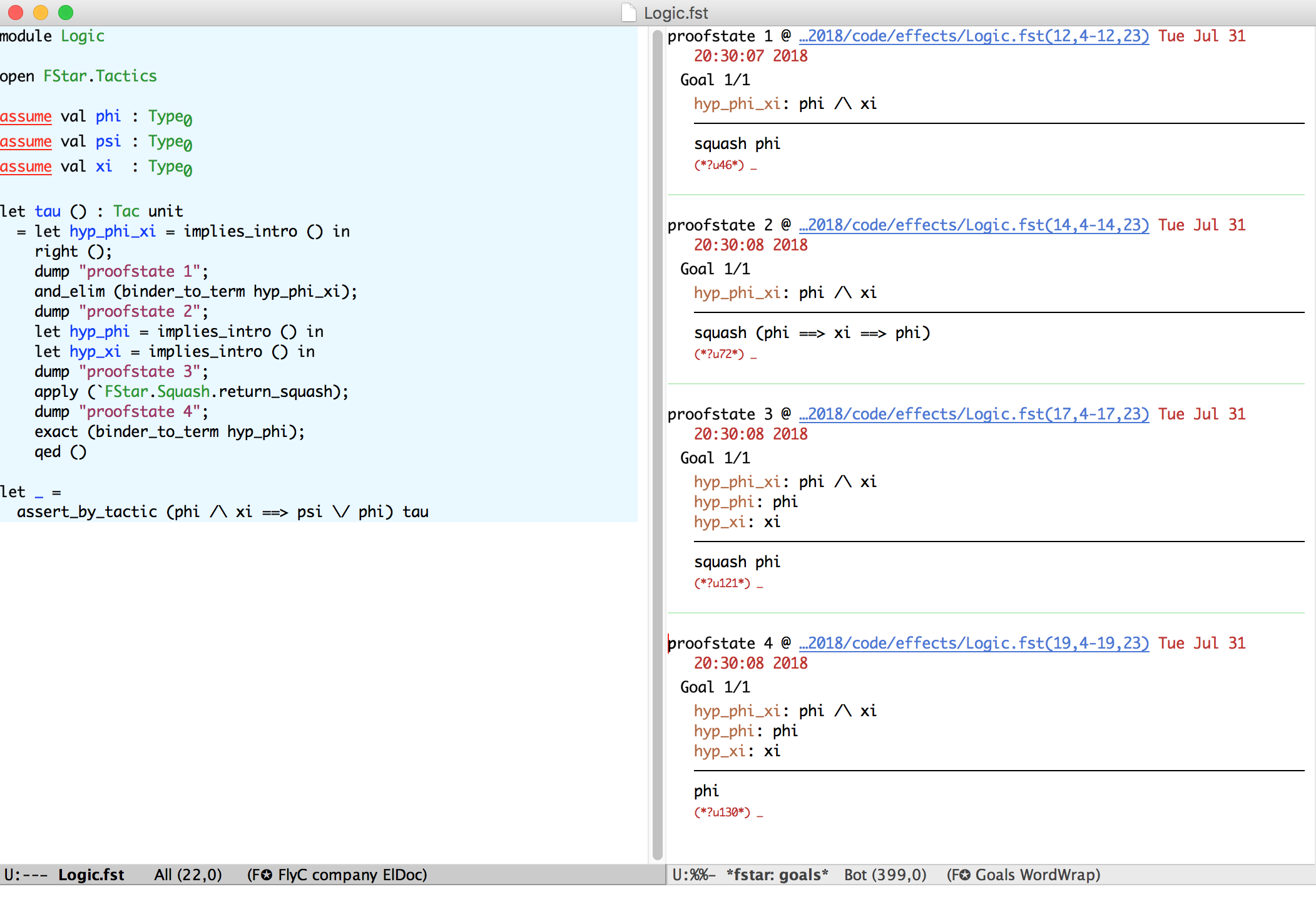
Tactics can massage verification conditions (complementing SMT)
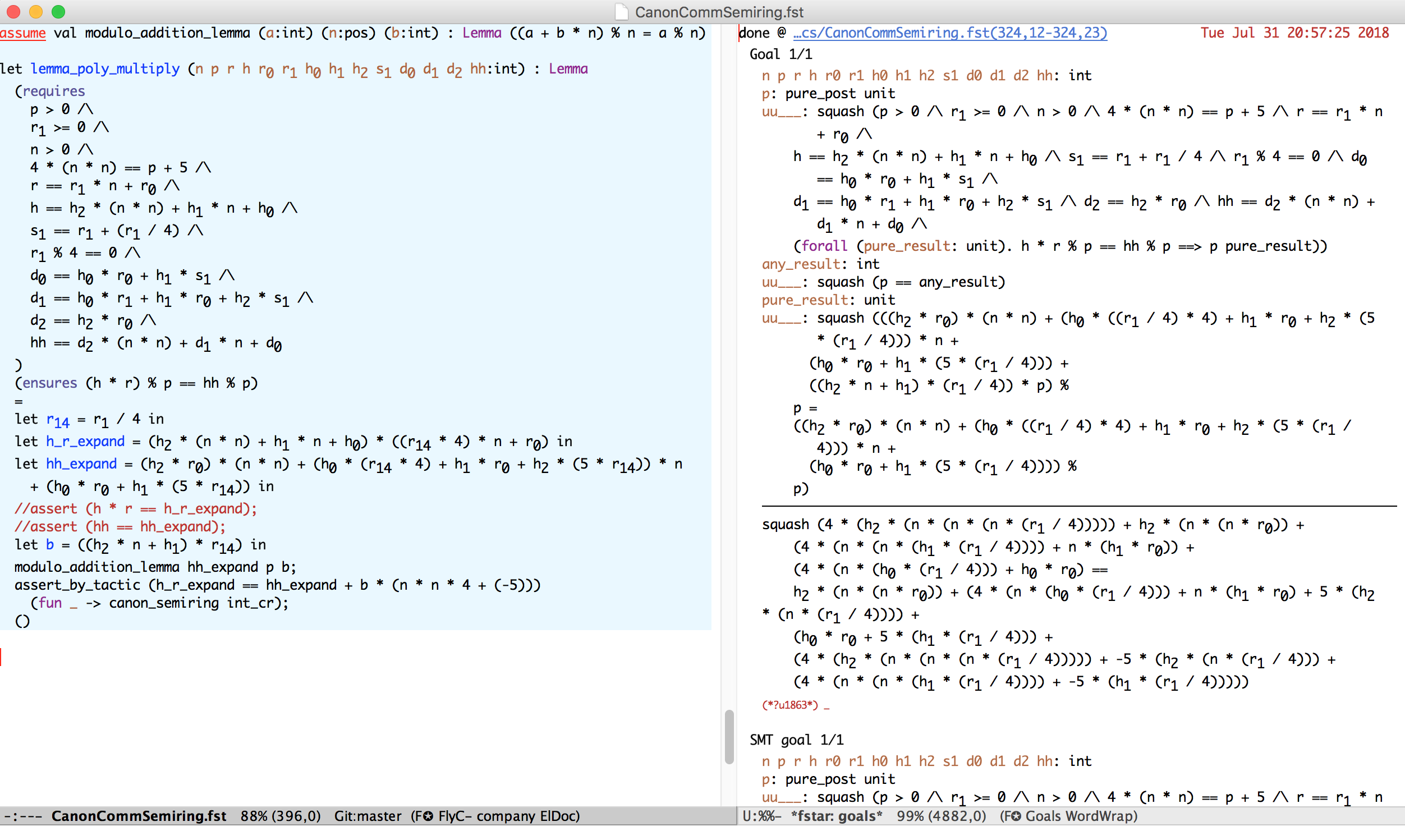
Tactics can synthesize F* terms (metaprogramming)
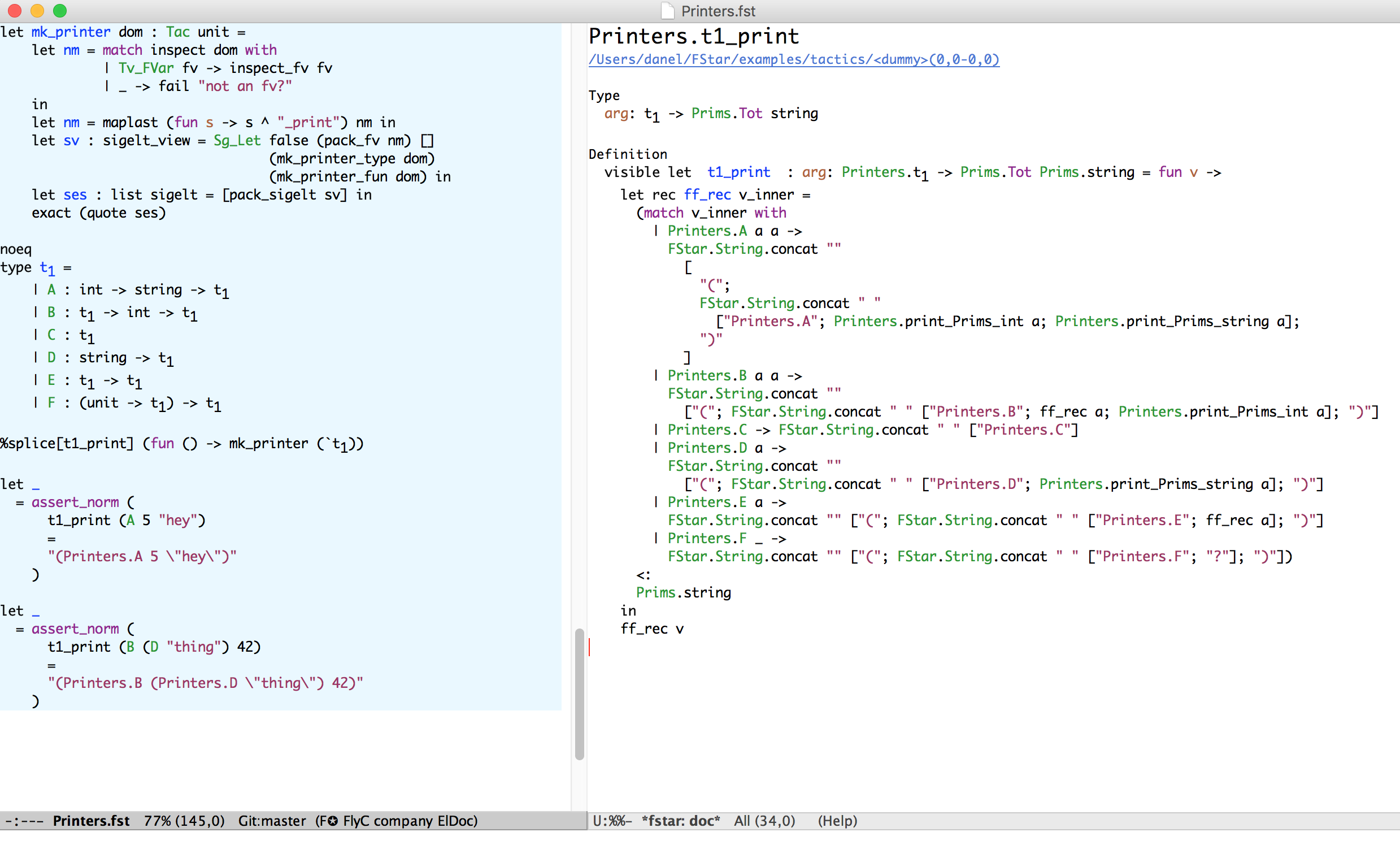
Tactics have also been used to extend F* with typeclasses