F*'s Extensible Effect System
and
Metaprogramming in F*

Schedule

• Friday: A Gentle Introduction to F* (Purely Functional Programs)

• Yesterday: Verifying Stateful Programs in F*

• Today: Monotonic State in F*

• Today: F*'s Extensible Effect System and Metaprogramming in F*

This talk

• Monadic effects in F*

• Verifying effectful programs extrinsically (monadic reification)

• Under the hood: Weakest preconditions (and Dijkstra monads)

• Tactics and Metaprogramming as a user-defined, non-primitive effect

Monadic effects in F*: Global State

type st (mem:Type) (a:Type) = mem -> Tot (a * mem)

total reifiable new_effect {
  STATE_m (mem:Type) : a:Type -> Effect
 
  with (* functional representation of the global state effect *)
       repr   = st mem;

       (* standard monadic return and bind for the state monad *)
       return = fun (a:Type) (x:a) (m:mem) -> (x, m);
       
       bind   = fun (a b:Type) (f:st mem a) (g:a -> st mem b) (m:mem) ->
                let (z, m') = f m in
                g z m';

       (* standard get and put actions for the state monad *)
       get    = fun () (m:mem) -> (m, m);
       put    = fun (m:mem) _ -> ((), m)
}

total reifiable new_effect STATE = STATE_m heap

• this monadic definition is the model F* uses to verify stateful code
• state can be primitively implemented under the hood, or not

Programming with effects, in direct style

• In F* the programmer writes:

  let incr_and_assert () : STATE unit user_spec = 
    let x = get() in
    put (x + 1);
    assert (get() > x)

• Which is then made explicitly monadic via type and effect inference:

  let incr_and_assert () : STATE unit inferred_spec = 
    STATE.bind (STATE.get ()) (fun x -> 
    STATE.bind (STATE.put (x + 1)) (fun _ ->
    STATE.bind (STATE.get ()) (fun y ->
    STATE.return (assert (y > x)))))

• And the SMT-solver is asked to discharge the VC to typecheck it

  forall s0 k. user_spec s0 k ==> inferred_spec s0 k

Monadic lifts in F*: State + Exceptions

let stexn a = nat -> Tot ((either a string) * nat))

new_effect {
  STEXN: a:Type -> Effect
  with (* functional representation of the sum of state and exceptions monads *)
       repr    = stexn;

       (* standard monadic return and bind *)
       return  = fun (a:Type) (x:a) s0 -> (Inl x, s0);
       
       bind    = fun (a b:Type) (f:stexn a) (g:a -> stexn b) s0 ->
                    let (r,s1) = f s0 in
                    match r with
                    | Inl ret -> g ret s1
                    | Inr m -> (Inr m, s1)

       (* action of raising exceptions *)
       raise   = fun (a:Type) (msg:string) s0 -> (Inr msg, s0);
}

sub_effect STATE ~> STEXN {
  lift = fun (a:Type)
             (e:st nat a)                               (* st comp. *)
         ->
             fun s -> let (x,s1) = e s0 in (Inl x, s1)  (* stexn comp. *) }

Programming with multiple effects, in direct style

• In F* the programmer writes:

  ( / ) : int -> x:int{x<>0} -> Tot int
    
  let divide_by (x:int) : STEXN unit user_spec
    = if x <> 0 then put (get () / x)
                else raise "Divide by zero"

• Which is then elaborated to:

  let divide_by (x:int) : STEXN unit inferred_spec
    = if x <> 0 then STATE_STEXN.lift (STATE.bind (STATE.get()) (fun n ->
                                       STATE.put (n / x)))
                else STEXN.raise "Divide by zero"

• And the SMT-solver is asked to discharge the VC to typecheck it

  forall s0 k. user_spec s0 k ==> inferred_spec s0 k

Under the hood

Weakest preconditions (Dijkstra monads (for free))

Computation types indexed by predicate transformers

Pre- and postconditions are just syntactic sugar:

Pure t (pre : Type0) (post : t -> Type0)
  = PURE t (fun k -> pre /\ (forall y. post y ==> k y))
                        (* where k is the "true" postcondition,  
                           for which we compute the weakest precondition *)

val factorial : x:int -> Pure int (requires (x >= 0))
                                  (ensures  (fun y -> y >= 0))

val factorial : x:int -> PURE int (fun k -> x>=0 /\ (forall y. y>=0 ==> k y))

ST t (pre : nat -> Type0) (post : nat -> t -> nat -> Type0) 
  = STATE t (fun n0 k -> pre n0 /\ (forall x n1. post n0 x n1 ==> k x n1))

val incr : unit -> St unit (requires (fun n0 -> True))
                           (ensures  (fun n0 _ n1 -> n1 = n0 + 1))

val incr : unit -> STATE unit (fun n0 k -> k () (n0 + 1))

Computing weakest preconditions, by example

let incr () = STATE.bind (STATE.get()) (fun x -> STATE.put (x + 1))

• By inferring type for incr against following interface:

  STATE.get : unit -> STATE nat (STATE.get_wp ())
  
  STATE.put : n:nat -> STATE unit (STATE.put_wp n)
  
  STATE.bind : STATE 'a 'wa -> (x:'a -> STATE 'b ('wb x)) ->
                                             STATE 'b (STATE.bind_wp 'wa 'wb)

  … F* computes the weakest precondition for incr

  val incr : unit -> STATE unit inferred_wp

  inferred_wp = STATE.bind_wp (STATE.get_wp()) (fun x -> STATE.put_wp (x+1))
              = fun n0 k -> k () (n0 + 1)

• Generic way of computing weakest-preconditions for all effects
  • provided we have a monad structure on predicate transformers
  • instance of a more general structure of monad-graded monads

Predicate transformers monad for state

aka a Dijkstra monad for state

let STATE.wp t = (t -> nat -> Type0) -> (nat -> Type0)

val STATE.return_wp : 'a -> Tot (STATE.wp 'a)

val STATE.bind_wp : (STATE.wp 'a) -> ('a -> Tot (STATE.wp 'b)) ->
                                                          Tot (STATE.wp 'b)
                      
val STATE.get_wp : unit -> Tot (STATE.wp nat)
val STATE.put_wp : nat -> Tot (STATE.wp unit)

• whose implementation is given by:

  let STATE.return_wp v = fun p -> p v
  let STATE.bind_wp wp f = fun p -> wp (fun v -> f v p)
  let STATE.get_wp () = fun p n0 -> p n0 n0
  let STATE.put_wp n = fun p _ -> p () n

• and for a while we wrote such things by hand for each new effect;
  

• but this is quite tricky and comes with strong proof obligations
  (correctness with respect to effect definition, monad laws, …)

Dijkstra monads for free

STATE.wp t  = (t -> nat -> Type0) -> (nat -> Type0)

           ~= nat -> (t * nat -> Type0) -> Type0

• This can be automatically derived from the state monad transformer

  STATE.repr t = nat -> M (t * nat)

  by selective continuation-passing style (CPS) translation

  • M is the monad-argument of the monad transformer
  • it marks where the CPS-translation happens
  • type system (conservatively) restricts where the marker M can appear

• This works well for many natural examples of monadic effects:
  

  • STATE, EXN, STEXN, CONT, etc. (explicitly definable monad transformers)
  • ongoing work to try to extend this idea to a wider class of effects

• Summary: From a monadic effect definition we can derive a
  correct-by-construction weakest-precondition calculus for this effect.

Verifying effectful programs extrinsically

Monadic reification and monadic reflection

Verifying effectful programs

New way: extrinsically (by exposing pure monadic representation)

• Monadic reification

  STATE.reify : (St a) -> (nat -> Tot (a * nat))

• Monadic reflection takes us in the other direction

  STATE.reflect : (nat -> Tot (a * nat)) -> (St a)

• The above types are very much simplified, in their full generality:
  • reify sends a STATE comp. with a WP to a PURE comp. with a WP
  • reflect sends a PURE comp. with a WP to a STATE comp. with a WP

Extrinsic reasoning using reification and reflection

• Reification allows us to give weak specification to a program

  let incr () : St unit = STATE?.put (STATE?.get() + 1)

• and give an extrinsic proof of their correctness

  let lemma_incrs (s0:state)
    : Lemma (let (_,s1) = reify (incr ()) s0 in 
             s1 = s0 + 1)
  = ()

• Reflection allows us to write some code as pure

  let incr' (): St unit = STATE?.put (STATE?.reflect (fun s0 -> (s0,s0)) + 1)

• and it cancels out reification in verification

  let lemma_incrs' (s0:state)
    : Lemma (let (_,s1) = reify (incr' ()) s0 in 
             s1 = s0 + 1)
  = ()

Extrinsic reasoning using reification and reflection ctd.

• It also allows us to reason about different runs of the same program

  let state = int * int                             (* (high - low) values *)
  
  let st (a:Type) = state -> M (a * state)
  
  total reifiable reflectable new_effect {
    STATE : a:Type -> Effect
    with repr = st; ...
  }
  

    let incr (n:int) : St unit = 
      STATE?.put_low (STATE?.get_low() + n)
  
    let incr2 () : St unit = 
      if (STATE?.get_high() = 42) then (incr 2) else (incr 1; incr 1)
  
    let non_interference ()
      : Lemma (forall h0 h1 n. let (_,(h0',n' )) = reify (incr2 ()) (h0,n) in 
                               let (_,(h1',n'')) = reify (incr2 ()) (h1,n) in
                               n' = n'')
    = ()

• or even about different runs of different programs

Reification works pretty well

• Reducing effectful verification to pure verification

  • for which F* already has good support (i.e. SMT automation)

• Recent experiments using this for “relational verification”

  • correctness of program transformations
  • information flow control
  • proofs of algorithmic optimizations (memoization, union-find)
  • simple game-based cryptographic proofs

• Downside: reification doesn't play well with monotonic state

  • cannot naively safely reify the real STATE and Stack effects
  • doing it naively allows you to replay old states with recall
  • ongoing work to solve it based on hybrid modal logics
  • unfortunately reification also starts to act on the context

Metaprogramming in F*

Tactics as a user-defined, non-primitive effect

Tactics (New, Still Experimental)

• F* tactics written as effectful F* code (inspired by Lean, Idris)

• have access to F*'s proof state (and can efficiently roll it back)

• can introspect on F* terms (deep embedding, simply typed)

• can be interpreted by F*'s normaliser(s)

• or compiled to OCaml and used as native plugins

• user-defined, non-primitive effect: proof state + exceptions monad

    noeq type __result a =
        | Success of a * proofstate
        | Failed  of string * proofstate
  
    let __tac (a:Type) = proofstate -> Tot (__result a)
  
    (* reifiable *) new_effect {
      TAC : a:Type -> Effect
      with repr = __tac; ...
    }
  
    let tactic (a:Type) = unit -> Tac a

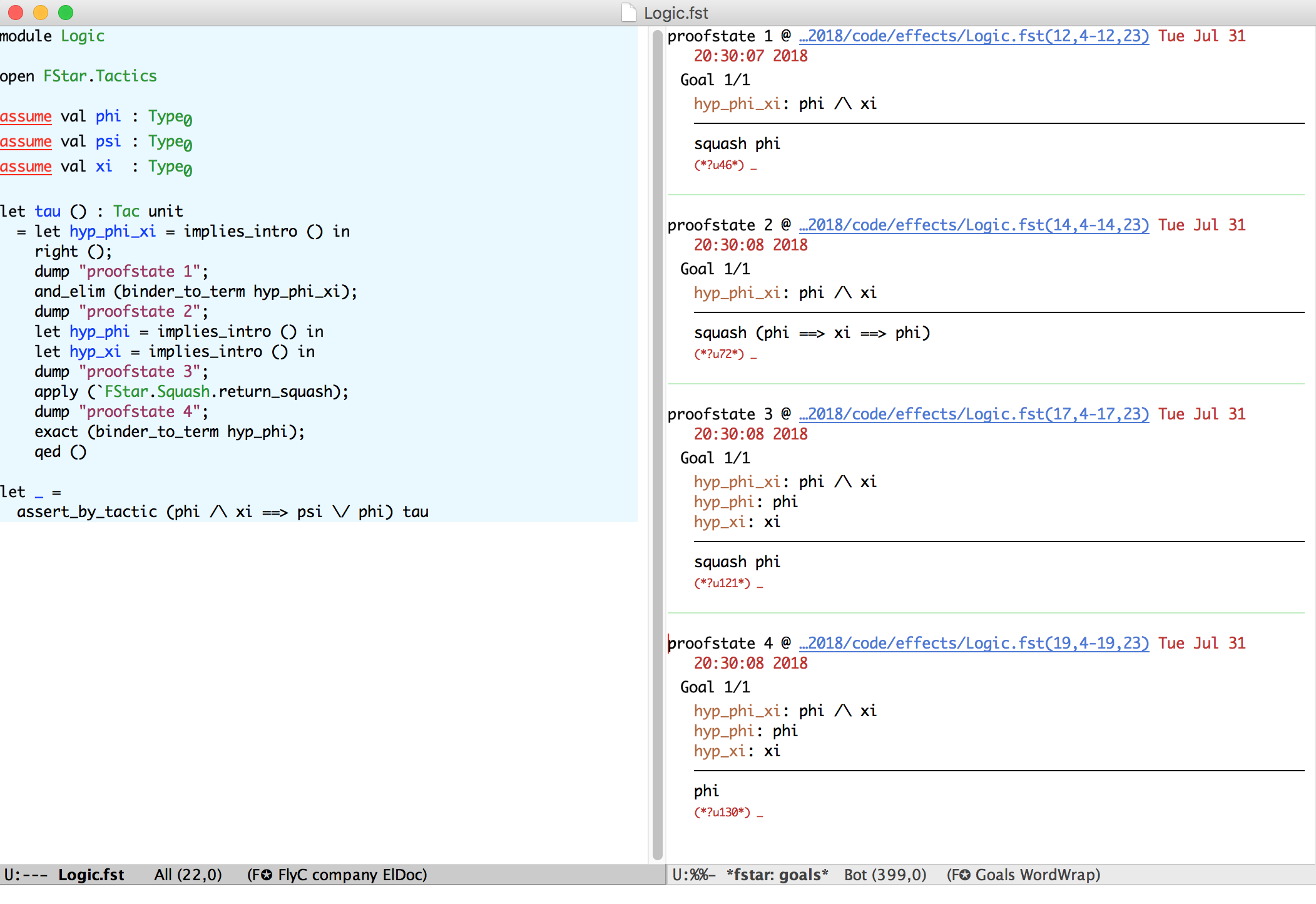
Tactics can discharge verification conditions (replacing SMT)

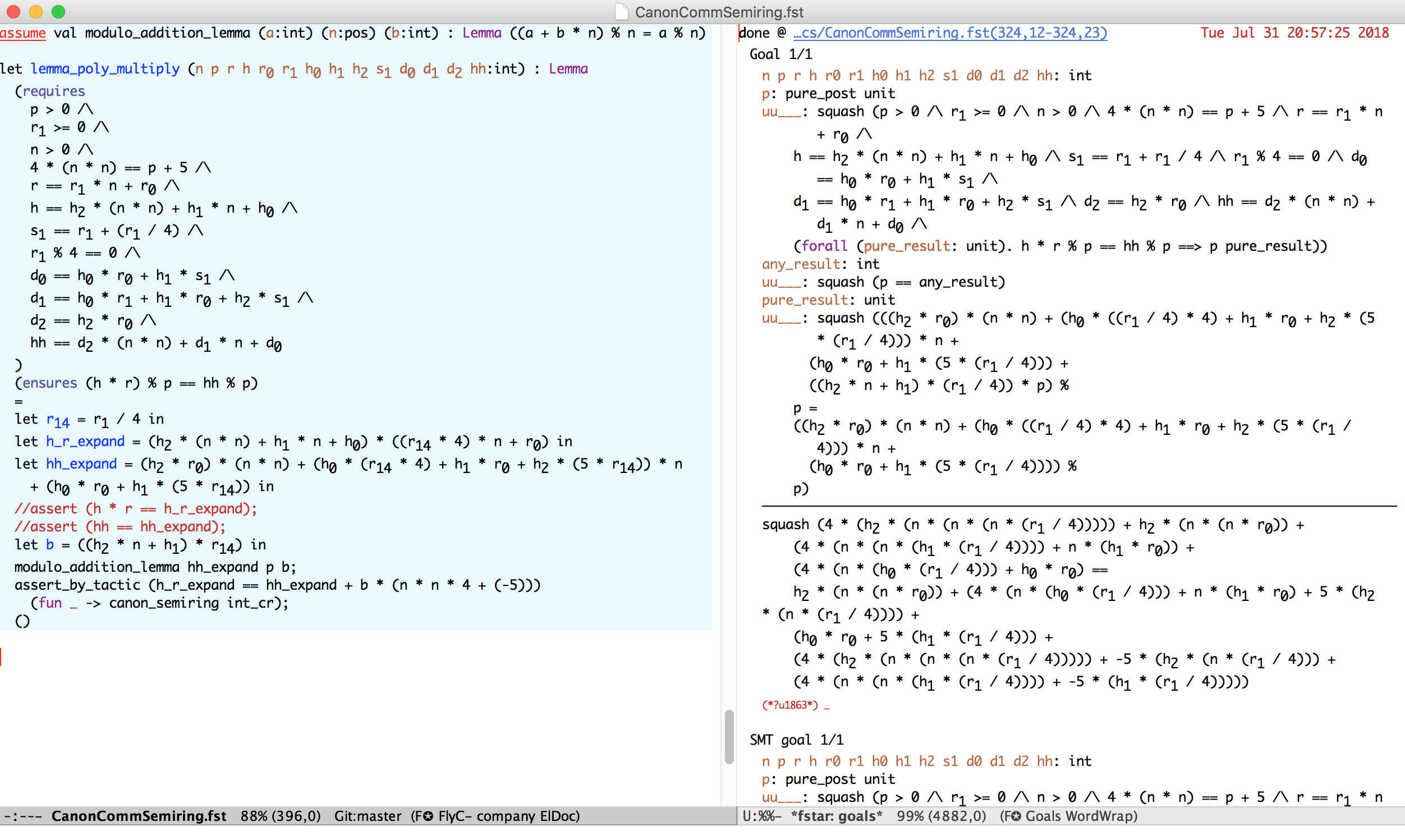
Tactics can massage verification conditions (complementing SMT)

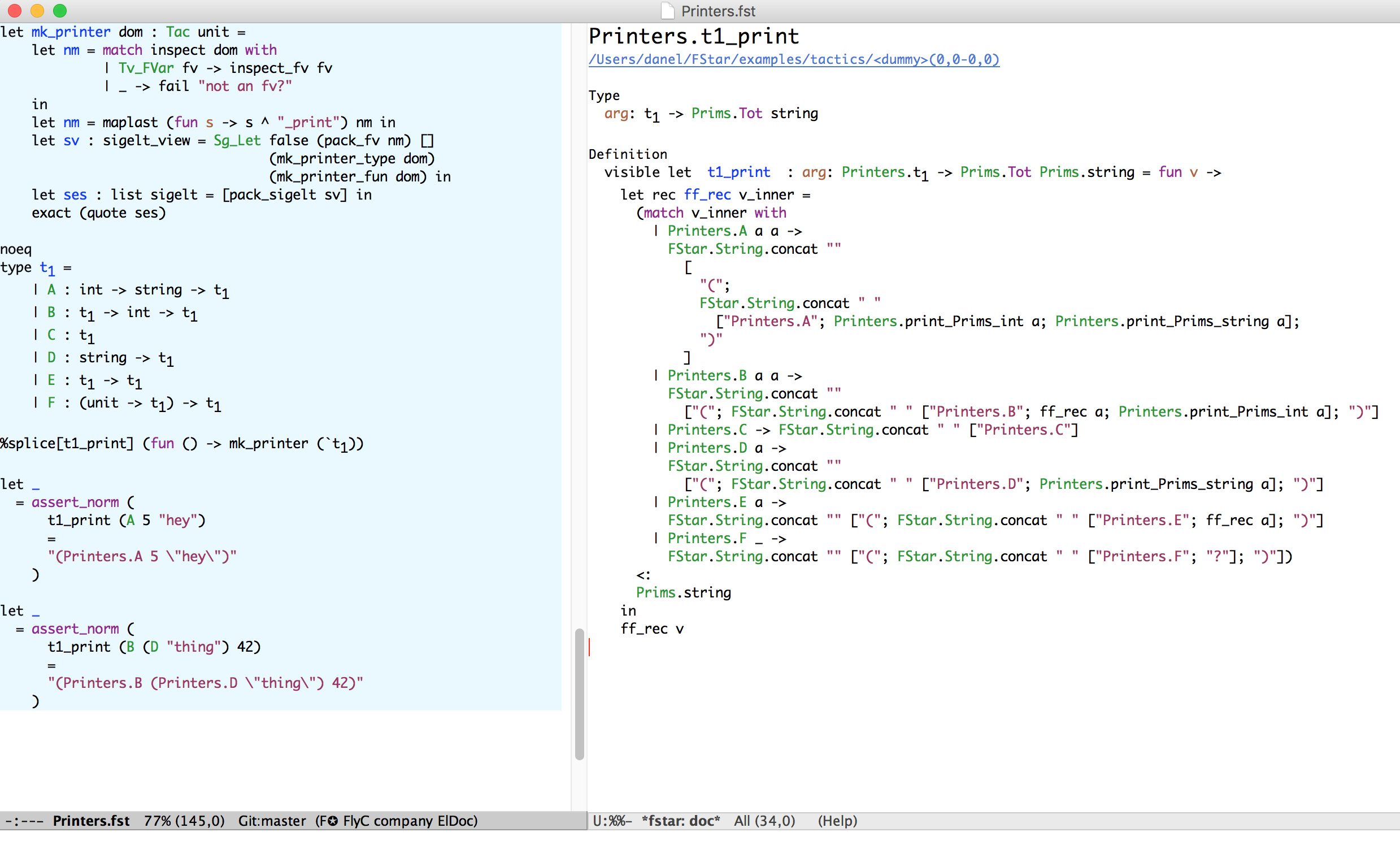
Tactics can synthesize F* terms (metaprogramming)

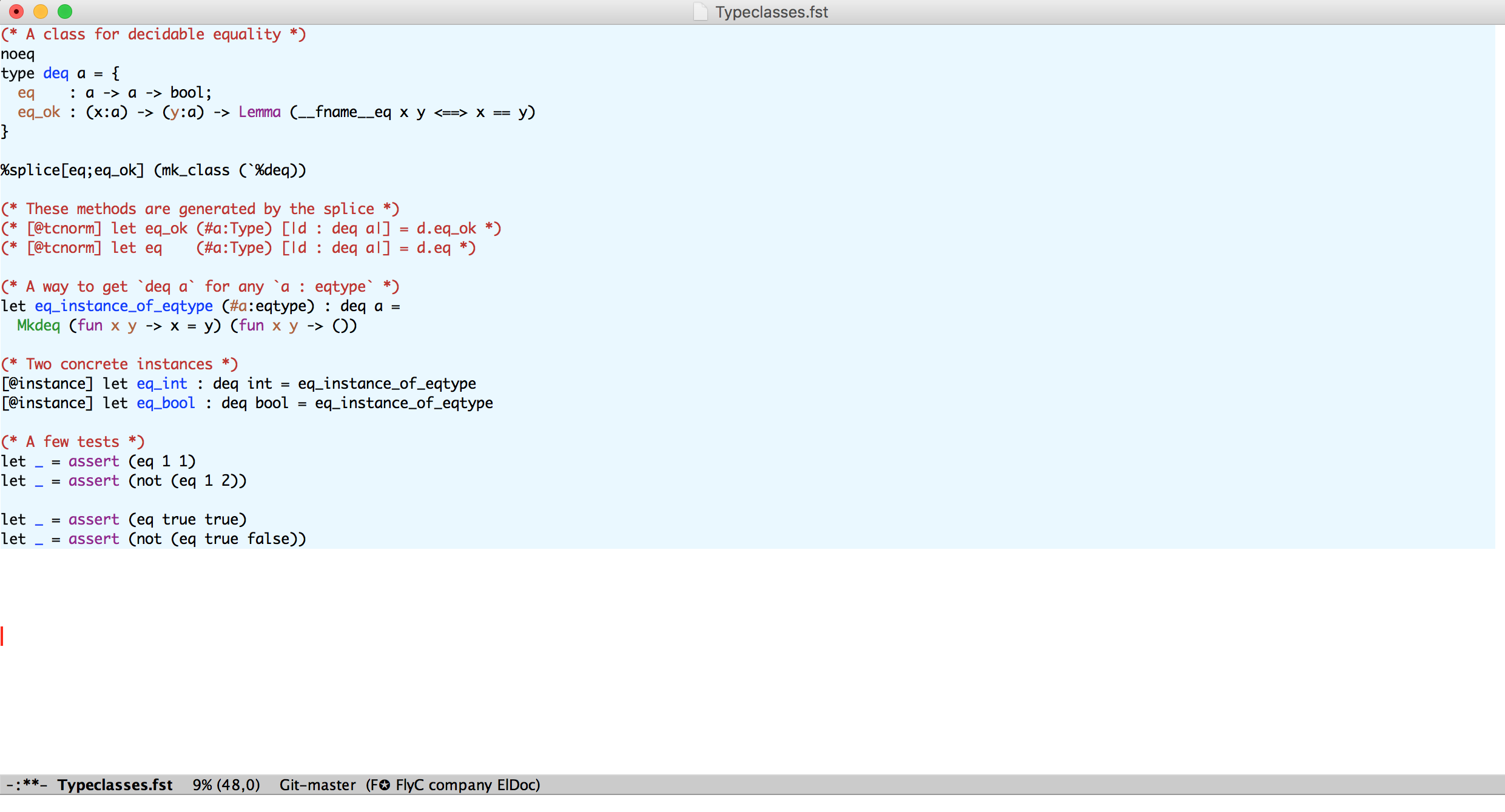
Tactics have also been used to extend F* with typeclasses

Some uses of tactics

• Reflective tactics for arithmetic (proof automation)

• Bitvectors in Vale (proof automation)

• Separation logic (proof automation)

• Pattern matcher (metaprogramming)

• Efficient low-level parsers and printers (metaprogramming)

Time to conclude!

• Friday: A Gentle Introduction to F* (Purely Functional Programs)

• Yesterday: Verifying Stateful Programs in F*

• Today: Monotonic State in F*

• Today: F*'s Extensible Effect System and Metaprogramming in F*